Advanced Calculus
of Several VariablesAdvanced Calculus
of Several VariablesC. H. EDWARDS, JR.The University of GeorgiaDOVER PUBLICATIONS, INC.New YorkCopyright Copyright 1973 by Academic Press, Inc. Bibliographical Note This Dover edition, first published in 1994, is an unabridged, corrected republication of the work first published by Academic Press, New York, 1973. Library of Congress Cataloging-in-Publication Data Edwards, C. (Charles Henry), 1937 Advanced calculus of several variables / C.H. (Charles Henry), 1937 Advanced calculus of several variables / C.H.
Edwards, Jr.
p. cm. Originally published: New York: Academic Press, 1973. Includes bibliographical references and index. ISBN-13: 978-0-486-68336-2 (pbk.) ISBN-10: 0-486-68336-2 (pbk.) 1. I. Title. Title.
QA303.E22 1994 515.84dc20 94-24204
CIP Manufactured in the United States by Courier Corporation
68336207
www.doverpublications.com To My ParentsCONTENTSPREFACE This book has developed from juniorsenior level advanced calculus courses that I have taught during the past several years. It was motivated by a desire to provide a modern conceptual treatment of multivariable calculus, emphasizing the interplay of geometry and analysis via linear algebra and the approximation of nonlinear mappings by linear ones, while at the same time giving equal attention to the classical applications and computational methods that are responsible for much of the interest and importance of this subject. In addition to a satisfactory treatment of the theory of functions of several variables, the reader will (hopefully) find evidence of a healthy devotion to matters of exposition as suchfor example, the extensive inclusion of motivational and illustrative material and applications that is intended to make the subject attractive and accessible to a wide range of typical science and mathematics students. The many hundreds of carefully chosen examples, problems, and figures are one result of this expository effort. This book is intended for students who have completed a standard introductory calculus sequence. A slightly faster pace is possible if the students' first course included some elementary multivariable calculus (partial derivatives and multiple integrals).
However this is not essential, since the treatment here of multivariable calculus is fully self-contained. We do not review single-variable calculus; with the exception of Taylor's formula in . might (depending upon the taste of the instructor) best be used as a source for reference as needed. treat multivariable integral calculus. In we treat the fundamental existence theorems of multivariable calculus by the method of successive approximations. builds upon the preceding chapters to give a comprehensive treatment, from the viewpoint of differential forms, of the classical material associated with line and surface integrals, Stokes' theorem, and vector analysis. builds upon the preceding chapters to give a comprehensive treatment, from the viewpoint of differential forms, of the classical material associated with line and surface integrals, Stokes' theorem, and vector analysis.
Here, as throughout the book, we are not concerned solely with the development of the theory, but with the development of conceptual understanding and computational facility as well. The remainder of the Chapter treats variational problems by the basic method of ordinary calculusequate the first derivative to zero, and then solve for the unknown (now a function). The method of Lagrange multipliers is generalized so as to deal in this context with the classical isoperimetric problems. There is a sense in which the exercise sections may constitute the most important part of this book. Although the mathematician may, in a rapid reading, concentrate mainly on the sequence of definitions, theorems and proofs, this is not the way that a textbook is read by students (nor is it the way a course should be taught). The student's actual course of study may be more nearly defined by the problems than by the textual material.
Consequently, those ideas and concepts that are not dealt with by the problems may well remain unlearned by the students. For this reason, a substantial portion of my effort has gone into the approximately 430 problems in the book. These are mainly concrete computational problems, although not all routine ones, and many deal with physical applications. A proper emphasis on these problems, and on the illustrative examples and applications in the text, will give a course taught from this book the appropriate intuitive and conceptual flavor. I wish to thank the successive classes of students who have responded so enthusiastically to the class notes that have evolved into this book, and who have contributed to it more than they are aware. Advanced Calculus
of Several VariablesI Euclidean Space and Linear Mappings Introductory calculus deals mainly with real-valued functions of a single variable, that is, with functions from the real line 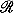 to itself. Advanced Calculus
to itself. Advanced Calculus
of Several VariablesI Euclidean Space and Linear Mappings Introductory calculus deals mainly with real-valued functions of a single variable, that is, with functions from the real line 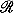 to itself.
to itself.
Multivariable calculus deals in general, and in a somewhat similar way, with mappings from one Euclidean space to another. However a number of new and interesting phenomena appear, resulting from the rich geometric structure of n-dimensional Euclidean space 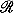 n. In this chapter we discuss
n. In this chapter we discuss 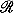 n in some detail, as preparation for the development in subsequent chapters of the calculus of functions of an arbitrary number of variables. This generality will provide more clear-cut formulations of theoretical results, and is also of practical importance for applications. For example, an economist may wish to study a problem in which the variables are the prices, production costs, and demands for a large number of different commodities; a physicist may study a problem in which the variables are the coordinates of a large number of different particles. Thus a real-life problem may lead to a high-dimensional mathematical model.
n in some detail, as preparation for the development in subsequent chapters of the calculus of functions of an arbitrary number of variables. This generality will provide more clear-cut formulations of theoretical results, and is also of practical importance for applications. For example, an economist may wish to study a problem in which the variables are the prices, production costs, and demands for a large number of different commodities; a physicist may study a problem in which the variables are the coordinates of a large number of different particles. Thus a real-life problem may lead to a high-dimensional mathematical model.
Fortunately, modern techniques of automatic computation render feasible the numerical solution of many high-dimensional problems, whose manual solution would require an inordinate amount of tedious computation. 1 THE VECTOR SPACE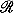 n As a set,
n As a set, 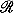 n is simply the collection of all ordered n-tuples of real numbers. That is,
n is simply the collection of all ordered n-tuples of real numbers. That is,  Recalling that the Cartesian product A B of the sets A and B is by definition the set of all pairs (a, b) such that
Recalling that the Cartesian product A B of the sets A and B is by definition the set of all pairs (a, b) such that 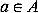 and
and 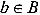 , we see that
, we see that 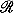 n can be regarded as the Cartesian product set
n can be regarded as the Cartesian product set 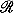
Next page















 to itself. Advanced Calculus
to itself. Advanced Calculus Recalling that the Cartesian product A B of the sets A and B is by definition the set of all pairs (a, b) such that
Recalling that the Cartesian product A B of the sets A and B is by definition the set of all pairs (a, b) such that 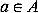 and
and 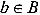 , we see that
, we see that