Mathematics discusses an enormous menagerie of mathematical objects: the number 28, the regular icosahedron, the finite field of size 169, the Gaussian distribution, and so on. It makes statements about them: 28 is a perfect number, the Gaussian distribution is symmetric about its mean. Yet it is not at all clear what kind of entity these objects are . Mathematical objects do not seem to be exactly like physical entities, like the Eiffel Tower; nor like fictional entities, like Hamlet; nor like socially constructed entities, like the English language or the US Senate; nor like structures arbitrarily imposed on the world, like the constellation Orion. Do mathematicians invent mathematical objects; or posit them; or discover them? Perhaps objects emerge of themselves, from the sea of mathematical thinking, or perhaps they come into being as we probe as suggested by Michael Dummett [].
Most of us who have done mathematics have at least the strong impression that the truth of mathematical statements is independent both of human choices, unlike truths about Hamlet, and of the state of the external world, unlike truths about the planet Venus. Though it has sometimes been argued that mathematical facts are just statements that hold by definition, that certainly doesnt seem to be the case; the fact that the number of primes less than N is approximately
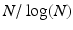
is certainly not in any way an obvious restatement of the definition of a prime number. Is mathematical knowledge fundamentally different from other kinds of knowledge or is it simply on one end of a spectrum of certainty?
Similarly, the truth of mathematicslike science in general, but even more stronglyis traditionally viewed as independent of the quirks and flaws of human society and politics. We know, however, that math has often been used for political purposes, often beneficent ones, but all too often to justify and enable oppression and cruelty. Most scientists would view such applications of mathematics as scientifically unwarranted; avoidable, at least in principle; and in any case irrelevant to the validity of the mathematics in its own terms. Others would argue that the validity of the mathematics in its own terms is an illusion and the phrase is propaganda; and that the study of mathematics, and the placing of mathematics on a pedestal, carry inherent political baggage. Freedom is the freedom to say that two plus two makes four wrote George Orwell, in a fiercely political book whose title is one of the most famous numbers in literature; was he right, or is the statement that two plus two makes four a subtle endorsement of power and subjection?
Concomitant with these general questions are many more specific ones. Are the integer 28, the real number 28.0, the complex number 28.0 + 0 i , the 1 1 matrix [28], and the constant function f ( x )=28 the same entity or different entities? Different programming languages have different answers. Is the integer 28 a single entity or a collection of similar entities; the signed integer, the whole number, the ordinal, the cardinal, and so on? Did Euler mean the same thing that we do when he wrote an integral sign? For that matter, do a contemporary measure theorist, a PDE expert, a numerical analyst, and a statistician all mean the same thing when they use an integral sign?
Such questions have been debated among philosophers and mathematicians for at least two and a half millennia. But, though the questions are eternal, the answers may not be. The standpoint from which we view these issues is significantly different from Hilbert and Poincar, to say nothing of Newton and Leibnitz, Plato and Pythagoras, reflecting the many changes the last century has brought. Mathematics itself has changed tremendously: vast new areas, new techniques, new modes of thought have opened up, while other areas have been largely abandoned. The applications and misapplications of mathematics to the sciences, technology, the arts, the humanities, and society have exploded. The electronic computer has arrived and has transformed the landscape. Computer technology offers a whole collection of new opportunities, new techniques, and new challenges for mathematical research; it also brings along its own distinctive viewpoint on mathematics.
The past century has also seen enormous growth in our understanding of mathematics and mathematical concepts as a cognitive and cultural phenomenon. A great deal is now known about the psychology and even the neuroscience of basic mathematical ability; about mathematical concepts in other cultures; about mathematical reasoning in children, in pre-verbal infants, and in animals.
Moreover the larger intellectual environment has altered, and with it, our views of truth and knowledge generally. Works such as Kuhns analysis of scientific progress and Foucaults analysis of the social aspects of knowledge have become part of the general intellectual currency. One can decide to reject them, but one cannot ignore them.
This book
The seventeen essays in this book address many different aspects of the ontology and meaning of mathematics from many different viewpoints. The authors include mathematicians, philosophers, computer scientists, cognitive psychologists, sociologists, historians, and educators. Some attack the ontological problem head on and propose a specific answer to the question, What is a mathematical object?; some attack it obliquely, by discussing related aspects of mathematical thought and practice; and some argue that the question is either useless or meaningless.
It would be both unnecessary and foolhardy to attempt to summarize the individual chapters. But it may be of interest to note some common themes:
The history of math, mathematical philosophy, and mathematical practice. (Avigad, Bailey & Borwein, Gillies, Gray, Ltzen, OHalloran, Martin & Pease, Ross, Stillwell, Verran). Among scientists, mathematicians are particularly aware of the history of their field; and philosophers sometimes seem to be aware of little else. Many different aspects and stages in the evolution of thinking about mathematics and its objects are traced in these different essays.
The real line and Euclidean geometry (Bailey & Borwein, Berlinski, E. Davis, Gillies, Gray, Ltzen, Stillwell). These essays in the collection touch on many different mathematical theories and objects, but the problems associated with
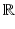
and
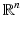
seem particularly prominent.
The role of language (Avigad, Azzouni, Gray, OHalloran, Piantadosi, Ross, Sinclair). On the one hand, mathematics itself seems to be something like a language; Ross discusses the view that mathematics is a universal or ideal language. On the other hand, a question like Do mathematical objects exist? is itself a linguistic expression; and it can be argued that difficulties of answering it derive from illusions about the precision or scope of language. Sinclair argues that we may be using the wrong language for mathematics; rather than thinking of mathematical entities as nouns, we should be thinking of them as verbs. Martin and Peases essay focuses on the related issue of communication in mathematical collaboration.










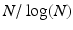 is certainly not in any way an obvious restatement of the definition of a prime number. Is mathematical knowledge fundamentally different from other kinds of knowledge or is it simply on one end of a spectrum of certainty?
is certainly not in any way an obvious restatement of the definition of a prime number. Is mathematical knowledge fundamentally different from other kinds of knowledge or is it simply on one end of a spectrum of certainty?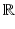 and
and 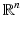 seem particularly prominent.
seem particularly prominent.