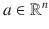Introduction
There is a rich literature in vision-based pose estimation driven by advances in the structure from motion in the field of computer vision [], that is systems with output in a projective space obtained as a quotient of the state space. Defining x as the position of the vehicle, the perspective outputs y ( x ) are of the form
and can be used to model the nonlinear projection along rays through the origin onto an affine image plane perpendicular to the focal axis of a classical perspective camera geometry. There are a number of works that consider filtering for
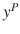
directly, rather than estimating the camera position [] using nonlinear techniques without requiring an additional state. The present chapter offers an extension and generalization of previous studies by the authors and deals in particular with single or multiple points with known or unknown location as well as velocity bias.
Rather than using the perspective outputs favoured in previous papers we use direction output representation of the measurement
corresponding to projection onto a virtual spherical image plane and differing from perspective outputs only in the scaling. The two formulations are essentially equivalent from a systems perspective in the region where perspective outputs are defined, however, we believe that the direction output representation contributes to the algebraic simplicity of the observer proposed in the present chapter. Much of the material presented in this chapter is already available in the literature, however, the focus on estimating the position as well as the bias in the measured velocity of an object moving in n (
)-dimensional Euclidean space from direction measurements changes the perspective and it is well worth covering the material again in a variety of situations while providing new solutions and new results in closely related cases. The structural question of observability is addressed and explicit and simple observability conditions are derived. The observers are designed first for the case of strong observability, corresponding to the situation in which the position can be algebraically obtained from at least 2 uniformly non-collinear directions to target-points with known locations. We then describe the proposed observer design methodology when a single observed point is considered. We characterize the observer convergence in terms of the persistence of excitation property and we provide some insights on the observers performance via a pseudo-Riccati equation introduced to improve the rate of convergence of the observer error to zero of the estimation error but also in order to estimate the eventual bias on the velocity measurement. The approach is then generalized to the case of multiple target-points with known location.
The SLAM problem is also considered as a natural extension of the proposed approach to estimate simultaneously the position of the vehicle and the relative location of the target-points involved in the measurements. We show in particular that the solutions we present in the chapter exploits a reduced dimension of the state and hence ensures a low computational complexity. To the authors knowledge, the solutions we proposed in the chapter have not been considered in the nonlinear observer literature. We provide rigorous proofs of the main results of the chapter as well as simulations to demonstrate the performance of the observers.
The chapter is organized in five sections. Following the present introduction, Sect..
Problem Statement
The motivating systems considered are the kinematics of a vehicle moving in two dimensions (the planar case) or in three dimensions (the spatial case). For the sake of generality, we will assume simply that the vehicle is moving in
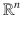
with
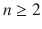
and develop a general theory. In this work, we consider the case where the orientation of the vehicle is known a-priori or separately estimated from a attitude observer . It follows that we can derotate all measurements and consider only inertial representations of position, velocity and direction. One has
where
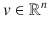
is the velocity of the object,
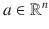














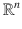 . The scenario considered assumes a possibly biased measurement of velocity along with bearing or direction measurements to one or multiple fixed points in the environment. The motivating example is a robot moving in either two- or three-dimensional space with a sensor, such as a camera , capable of providing bearing but not distance to observed fixed points in the environment. We provide a comprehensive observability analysis, and discuss stability and convergence of the observer design and observer error dynamics, under persistence of excitation conditions on the vehicle motion. Interestingly, we can show uniform observability even for a single direction measure and with unknown velocity bias as long as the vehicle trajectory is persistently exciting. Some extensions to the case of multiple directions with known- or unknown-observed point location are addressed and observers endowed with exponential stability of error dynamics are derived. Simulation results are presented that demonstrate the performance of the proposed approach.
. The scenario considered assumes a possibly biased measurement of velocity along with bearing or direction measurements to one or multiple fixed points in the environment. The motivating example is a robot moving in either two- or three-dimensional space with a sensor, such as a camera , capable of providing bearing but not distance to observed fixed points in the environment. We provide a comprehensive observability analysis, and discuss stability and convergence of the observer design and observer error dynamics, under persistence of excitation conditions on the vehicle motion. Interestingly, we can show uniform observability even for a single direction measure and with unknown velocity bias as long as the vehicle trajectory is persistently exciting. Some extensions to the case of multiple directions with known- or unknown-observed point location are addressed and observers endowed with exponential stability of error dynamics are derived. Simulation results are presented that demonstrate the performance of the proposed approach.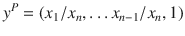
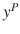 directly, rather than estimating the camera position [] using nonlinear techniques without requiring an additional state. The present chapter offers an extension and generalization of previous studies by the authors and deals in particular with single or multiple points with known or unknown location as well as velocity bias.
directly, rather than estimating the camera position [] using nonlinear techniques without requiring an additional state. The present chapter offers an extension and generalization of previous studies by the authors and deals in particular with single or multiple points with known or unknown location as well as velocity bias.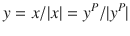
 )-dimensional Euclidean space from direction measurements changes the perspective and it is well worth covering the material again in a variety of situations while providing new solutions and new results in closely related cases. The structural question of observability is addressed and explicit and simple observability conditions are derived. The observers are designed first for the case of strong observability, corresponding to the situation in which the position can be algebraically obtained from at least 2 uniformly non-collinear directions to target-points with known locations. We then describe the proposed observer design methodology when a single observed point is considered. We characterize the observer convergence in terms of the persistence of excitation property and we provide some insights on the observers performance via a pseudo-Riccati equation introduced to improve the rate of convergence of the observer error to zero of the estimation error but also in order to estimate the eventual bias on the velocity measurement. The approach is then generalized to the case of multiple target-points with known location.
)-dimensional Euclidean space from direction measurements changes the perspective and it is well worth covering the material again in a variety of situations while providing new solutions and new results in closely related cases. The structural question of observability is addressed and explicit and simple observability conditions are derived. The observers are designed first for the case of strong observability, corresponding to the situation in which the position can be algebraically obtained from at least 2 uniformly non-collinear directions to target-points with known locations. We then describe the proposed observer design methodology when a single observed point is considered. We characterize the observer convergence in terms of the persistence of excitation property and we provide some insights on the observers performance via a pseudo-Riccati equation introduced to improve the rate of convergence of the observer error to zero of the estimation error but also in order to estimate the eventual bias on the velocity measurement. The approach is then generalized to the case of multiple target-points with known location.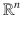 with
with 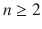 and develop a general theory. In this work, we consider the case where the orientation of the vehicle is known a-priori or separately estimated from a attitude observer . It follows that we can derotate all measurements and consider only inertial representations of position, velocity and direction. One has
and develop a general theory. In this work, we consider the case where the orientation of the vehicle is known a-priori or separately estimated from a attitude observer . It follows that we can derotate all measurements and consider only inertial representations of position, velocity and direction. One has 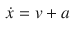
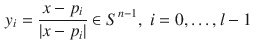
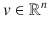 is the velocity of the object,
is the velocity of the object,