Table of Contents
Rich would like to dedicate this book to his daughter Nancy, age 4, in the hope that she can find a partial answer contained herein when she starts to wonder what he did when she was growing up. In the same spirit, Barry would like to dedicate this book to his daughter Devra, age 18, who for many years has been asking, What do you do at work, Daddy?, in the conviction that she will find in its contents a more satisfying answer than she has invariably received previously, specifically, I worry about stuff.
Acknowledgments
We would like to acknowledge our editors, Bill Falloon and Emilie Herman of Wiley, for their efforts and support; Sara Pick and Paige Lesniak for administrative support throughout the process; and Rebecca Lindsey (who is not a quant!) for her careful reading and editing of this work. Barry would like to thank Karen Hoogsteen, for her always-ready support, encouragement, and patience. Finally, we want to thank each of the contributors for taking time out of their busy lives to share their experiences.
Introduction
Because you are reading this introduction, one of four things must be true. You are a quant and are intrigued by the idea of reading the stories of others like you. You are not a quant, but aspire to quantness, and you are seeking some insight on how to achieve that goal. You are neither a quant, nor have such aspirations, but you want to understand the way Wall Street really works, perhaps to gain some perspective on the vast and unsympathetic forces affecting your life in mysterious ways. Or, misshelved among the science fiction and fantasy titles by a harried employee, the title has struck your fancy as, perhaps, a potentially satisfying space opera. There might be other things besides these four, but we cant think of any. For all of you except the fourth group, we are pretty sure this book will provide considerable satisfaction. (For the fourth group, who knows?) By way of introduction, we will explain from our perspective the roots, roles, and contributions of the Wall Street quant.
We begin by defining the
Quant. Mark Joshi, a famous quant, has proposed this definition:
A quant designs and implements mathematical models for the pricing of derivatives, assessment of risk, or predicting market movements.
Perhaps some of the terms used in this definition require definition themselves. A
mathematical model is a formula, equation, group of equations, or computational algorithm that attempts to explain some type of relationship. For example, Einsteins famous
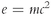
is a model that describes the relationship between energy and mass.
Quants implement models that focus on financial relationships. Perhaps the most famous of these is the Black-Scholes option pricing formula, which describes the relationship between the prices of two financial instruments that have a particular connection. The development of the Black-Scholes model (between 1969 and 1973) is often cited as one of the factors that started the quant revolution on Wall Street, but that is an oversimplification.
Returning to the definition of a quant, the derivatives for which quants design models are financial instruments whose values depend on (or are determined by) the future value of some quantity. This definition may seem vagueand it is. Derivatives exist in such variety that any definition hoping to be all-encompassing has to be vague.
One concrete and ubiquitous example of a derivative is an equity call option (a call). Someone who buys a call has purchased the future right to buy the specified companys common shares, not at the market price, but at the price stated in the option contract.
Options have been around for a long time, but one date is commonly cited as the trigger for the derivatives revolution (which is inextricably associated with the quant revolution). That date is April 26, 1973, though to call this the beginning of the derivatives revolution is an oversimplification. On this date there was an earthquake off the coast of Hawaii, but the real earthquake that day was in Chicago. The Chicago Board Options Exchange (CBOE) became the first organized exchange to have regular trading in equity options. A humble beginning, certainly, as only 911 option contracts were traded on 16 different equities. Now, each year, hundreds of millions of equity option contracts on thousands of companies trade on dozens of exchanges (both physical and electronic) around the world.
The key ingredient that ties quants to derivatives and the other two functions identified by Joshi (risk assessment and predicting markets) is mathematical know-how. The Black-Scholes option pricing formula is a good example of this.
The model, as it was first presented, was obtained by employing a result from physics, the solution to a particular partial differential equation called the heat-transfer equation. The level of abstractness involved in this work frequently inspires awe, fear, and even derision among nonquants. Consider this quotation from Time magazine of April 1994, cited by Peter Bernstein: Prices of derivatives are not based on old-fashioned human hunches but on calculations designed and monitored by computer wizards using abstruse mathematical formulas... developed by so-called quants...
Wizards, indeed. Even Emanuel Derman, one of the most famous of quants, feels compelled to assert that [t]he Black-Scholes model tells us, almost miraculously, how to manufacture an option... (italics added).
As the knowledge necessary to perform such feats is not a part of the regular secondary-school math curriculum, facility with derivatives requires a level of quantitative (hence quant) training and skill confined to the mathematical specialist.
Where can these specialists be found? For Wall Street, the breeding grounds of future quants are the halls of academe, and more specifically, graduate departments of physics, mathematics, engineering, and (to a lesser extent) finance and economics. The favored candidates are holders of the degree of PhD, but not exclusively so. More recently, a new breeding ground of quants has arisen in schools that have begun teaching more focused curricula, leading to masters in quantitative finance, masters in financial engineering, masters in computational finance, and masters in mathematical finance, for example.
Okaythe reader will now be asking, So thats what quants do and where they come from, but why do they do it? The obvious answer, as you readers of the second group have already figured out, is that being a quant is financially rewarding. It is financially rewarding because a quant produces something with significant utility in the financial marketplace. Still, such an answer would have been greeted with derision by the famous mathematician G. H. Hardy. In his apologia to mathematics research he states,
The real mathematics of the real mathematicians, the mathematics of Fermat and Euler and Gauss and Abel and Riemann, is almost wholly useless... It is not possible to justify the life of any genuine professional mathematician on the ground of the utility of his work.
But before we weep for quants who, while well-rewarded financially, have failed to justify their lives when measured by Hardys yardstick, it must be noted that the yardstick has a crack in it. The work of two of Hardys icons, Pierre Fermat and Frederick Gauss, perhaps above all other mathematicians, have contributed to the utility of quants efforts.










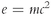 is a model that describes the relationship between energy and mass.
is a model that describes the relationship between energy and mass.