John D. Barrow - 100 Essential Things You Didnt Know You Didnt Know

Contents

About the Book

If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is. John von Neumann

Mathematics can tell you things about the world that cant be learned in any other way. This hugely informative and wonderfully entertaining little book answers one hundred essential questions about existence. It unravels the knotty, clarifies the conundrums and sheds light into dark corners. From winning the lottery, placing bets at the races and escaping from bears to sports, Shakepeare, Google, game theory, drunks, divorce settlements and dodgy accounting; from chaos to infinity and everything in between, 100 Essential Things You Didnt Know You Didnt Know has all the answers!

About the Author

John D. Barrow is Professor of Mathematical Sciences and Director of the Millenium Mathematics Project at Cambridge University, Fellow of Clare Hall, Cambridge, a Fellow of the Royal Society, and the current Gresham Professor of Geometry at Gresham College, London. His previous books include The Origin of the Universe; The Universe that Discovered Itself; The Book of Nothing; The Constants of Nature: From Alpha to Omega; The Infinite Book: A Short Guide to the Boundless, Timeless and Endless; The Artful Universe Expanded; New Theories of Everything and, most recently, Cosmic Imagery: Key Images in the History of Science. He is also the author of the award-winning play Infinities.

Also by John Barrow

Theories of Everything

The Left Hand of Creation

(with Joseph Silk)

LHomme et le Cosmos

(with Frank J. Tipler)

The Anthropic Cosmological Principle

(with Frank J. Tipler)

The World within the World

The Artful Universe

Pi in the Sky

Perch il mondo matematico?

Impossibility

The Origin of the Universe

Between Inner Space and Outer Space

The Universe that Discovered Itself

The Book of Nothing

The Constants of Nature:

From Alpha to Omega

The Infinite Book:

A Short Guide to the Boundless,

Timeless and Endless

Cosmic Imagery:

Key Images in the History of Science

100 Essential Things You Didnt Know

You Didnt Know About Sport

The Book of Universes

To David and Emma

I continued to do arithmetic with my father, passing proudly through fractions to decimals. I eventually arrived at the point where so many cows ate so much grass, and tanks filled with water in so many hours. I found it quite enthralling.

Agatha Christie

Preface

This is a little book of bits and pieces bits about off-beat applications of mathematics to everyday life, and pieces about a few other things not so very far away from it. There are a hundred to choose from, in no particular order, with no hidden agenda and no invisible thread. Sometimes you will find only words, but sometimes you will find some numbers as well, and very occasionally a few further notes that show you some of the formulae behind the appearances. Maths is interesting and important because it can tell you things about the world that you cant learn in any other way. When it comes to the depths of fundamental physics or the breadth of the astronomical universe we have almost come to expect that. But I hope that here you will see how simple ideas can shed new light on all sorts of things that might otherwise seem boringly familiar or just pass by unnoticed.

Lots of the examples contained in the pages to follow were stimulated by the goals of the Millennium Mathematics Project, which I came to Cambridge to direct in 1999. The challenge of showing how mathematics has something to tell about most things in the world around us is one that, when met, can play an important part in motivating and informing people, young and old, to appreciate and understand the place of mathematics at the root of our understanding of the world.

I would like to thank Steve Brams, Marianne Freiberger, Jenny Gage, John Haigh, Jrg Hensgen, Helen Joyce, Tom Krner, Imre Leader, Drummond Moir, Robert Osserman, Jenny Piggott, David Spiegelhalter, Will Sulkin, Rachel Thomas, John H. Webb, Marc West, and Robin Wilson for helpful discussions, encouragement, and other practical inputs that contributed to the final collection of essential things you now find before you.

Finally, thanks to Elizabeth, David, Roger and Louise for their unnervingly close interest in this book. Several of these family members now often tell me why pylons are made of triangles and tightrope walkers carry long poles. Soon you will know too.

John D. Barrow

August 2008, Cambridge

Pylon of the Month

Like Moses parting the waves, National Grid Company PLCs 4YG8 leads his fellow pylons through this Oxfordshire housing estate towards the promised land of Didcot Power Station.

The December 1999 Pylon of the Month

There are some fascinating websites about, but none was more beguiling than the iconic Pylon of the Month, once devoted to providing monthly pin-ups of the worlds most exciting and seductive electricity pylons. The ones shown on the website below are from Scotland. Alas, Pylon of the Month now seems to have become a cobweb site, but there is still something to learn from it, since for the mathematician every pylon tells a story. It is about something so prominent and ubiquitous that, like gravity, it goes almost unnoticed.

Next time you go on a train journey, look carefully at the pylons as they pass swiftly by the windows. Each is made of a network of metal struts that make use of a single recurring polygonal shape. That shape is the triangle. There are big triangles and smaller ones nested within them. Even apparent squares and rectangles are merely separate pairs of triangles. The reason forms a small part of an interesting mathematical story that began in the early nineteenth century with the work of the French mathematician Augustin-Louis Cauchy.

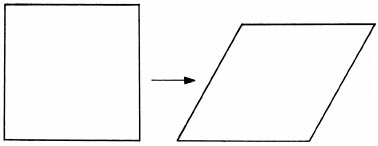
Of all the polygonal shapes that we could make by bolting together straight struts of metal, the triangle is special. It is the only one that is rigid. If they were hinged at their corners, all the others can be flexed gradually into a different shape without bending the metal. A square or a rectangular frame provides a simple example: we see that it can be deformed into a parallelogram without any buckling. This is an important consideration if you aim to maintain structural stability in the face of winds and temperature changes. It is why pylons seem to be great totems to the god of all triangles.

If we move on to three-dimensional shapes then the situation is quite different: Cauchy showed that every convex polyhedron (i.e. in which the faces all point outwards) with rigid faces, and hinged along its edges, is rigid. And, in fact, the same is true for convex polyhedra in spaces with four or more dimensions as well.

What about the non-convex polyhedra, where some of the faces can point inwards? They look much more squashable. Here, the question remained open until 1978 when Robert Connelly found an example with non-convex faces that is not rigid and then showed that in all such cases the possible flexible shifts keep the total volume of the polyhedron the same. However, the non-convex polyhedral examples that exist, or that may be found in the future, seem to be of no immediate practical interest to structural engineers because they are special in the sense that they require a perfectly accurate construction, like balancing a needle on its point. Any deviation from it at all just gives a rigid example, and so mathematicians say that almost every polyhedron is rigid. This all seems to make structural stability easy to achieve but pylons do buckle and fall down. Im sure you can see why.