Barrow - 100 essential things you didnt know you didnt know: math explains your world

This is a little book of bits and piecesbits about off-beat applications of mathematics to everyday life, and pieces about a few other things not so very far away from it. There are a hundred to choose from, in no particular order, with no hidden agenda and no invisible thread. Sometimes you will find only words, but sometimes you will find some numbers as well, and very occasionally a few further notes that show you some of the formulae behind the appearances. Maths is interesting and important because it can tell you things about the world that you cant learn in any other way. When it comes to the depths of fundamental physics or the breadth of the astronomical universe we have almost come to expect that. But I hope that here you will see how simple ideas can shed new light on all sorts of things that might otherwise seem boringly familiar or just pass by unnoticed.

Lots of the examples contained in the pages to follow were stimulated by the goals of the Millennium Mathematics Project, which I came to Cambridge to direct in 1999. The challenge of showing how mathematics has something to tell about most things in the world around us is one that, when met, can play an important part in motivating and informing people, young and old, to appreciate and understand the place of mathematics at the root of our understanding of the world.

I would like to thank Steve Brams, Marianne Freiberger, Jenny Gage, John Haigh, Jrg Hensgen, Helen Joyce, Tom Krner, Imre Leader, Drummond Moir, Robert Osserman, Jenny Piggott, David Spiegelhalter, Will Sulkin, Rachel Thomas, John H. Webb, Marc West, and Robin Wilson for helpful discussions, encouragement, and other practical inputs that contributed to the final collection of essential things you now find before you.

Finally, thanks to Elizabeth, David, Roger and Louise for their unnervingly close interest in this book. Several of these family members now often tell me why pylons are made of triangles and tightrope walkers carry long poles. Soon you will know too.

John D. Barrow

August 2008, Cambridge

Two people who get on well together can often find their relationship destabilised by the arrival of a third into their orbit. This is even more noticeable when gravity is the force of attraction involved. Newton taught us that two masses can remain in stable orbit around their centre of mass under their mutual gravitational forcesas do the Earth and the Moon. But if a third body of similar mass is introduced into the system, then something quite dramatic generally happens. One body finds itself kicked out of the system by the gravitational forces, while the two that remain are drawn into a more tightly bound stable orbit.

This simple slingshot process is the source of a fantastic counter-intuitive property of Newtons theory of gravity discovered by Jeff Xia in 1992. First, take four particles of equal mass M and arrange them in two pairs orbiting within two planes that are parallel and with opposite directions of spin so there is no overall rotation. Now introduce a fifth much lighter particle m that oscillates back and forth along the perpendicular through the mass centres of the two pairs. The group of five particles will expand to infinite size in a finite time!

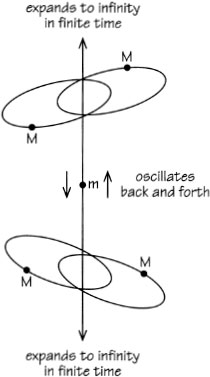
How does this happen? The little oscillating particle runs from one pair to the other, and at the other it creates a little 3-body problem and gets ejected, and the pair recoils outwards to conserve momentum. The lightest particle then travels across to the other pair and the same scenario is repeated. This happens time and time again, without end, and accelerates the two pairs so hard that they become infinitely separated in a finite time, undergoing an infinite number of oscillations in the process.

This example actually solves an old problem posed by philosophers as to whether it is possible to perform an infinite number of actions in a finite time. Clearly, in a Newtonian world where there is no speed limit, it is. Unfortunately (or perhaps fortunately), this behaviour is not possible when Einsteins relativity is taken into account. No information can be transmitted faster than the speed of light and gravitational forces cannot become arbitrarily strong in Einsteins theory of motion and gravitation. Nor can masses get arbitrarily close to each other and recoil. When two masses of mass M get closer than a distance 4GM/c2, where G is Newtons gravitation constant and c is the speed of light, then a horizon surface of no-return forms around them and they form a black hole from which they cannot escape.

The slingshot effect of gravity can be demonstrated in your back garden with a simple experiment. It shows how three bodies can combine to create big recoil as they try to conserve momentum when they pass close to each other (in the case of astronomical bodies) or collide (as it will be in our experiment).

The three bodies will be the Earth, a large ball (like a basket ball or smooth-surfaced football) and a small ball (like a ping-pong or tennis ball). Hold the small ball just above the large ball at about chest height and let them both fall to the ground together. The big ball will hit the ground first and rebound upwards, hitting the small ball while it is still falling. The result is rather dramatic. The small ball bounces up to a height about nine times higher than it would have gone if it had just been dropped on the ground from the same height. You might not want to do this indoors!