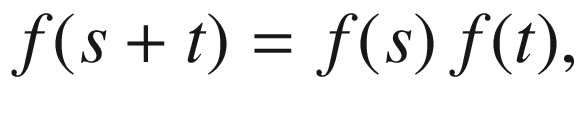Jacek Banasiak - Semigroups of Operators - Theory and Applications. SOTA, Kazimierz Dolny, Poland, September/October 2018

Springer Proceedings in Mathematics & Statistics

This book series features volumes composed of selected contributions from workshops and conferences in all areas of current research in mathematics and statistics, including operation research and optimization. In addition to an overall evaluation of the interest, scientific quality, and timeliness of each proposal at the hands of the publisher, individual contributions are all refereed to the high quality standards of leading journals in the field. Thus, this series provides the research community with well-edited, authoritative reports on developments in the most exciting areas of mathematical and statistical research today.

More information about this series at http://www.springer.com/series/10533

This Springer imprint is published by the registered company Springer Nature Switzerland AG

The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland

The presented volume is, to some extent, a sequel to the book of proceedings Semigroups of Operators: Theory and Applications published in 2015. They both contain selected, peer-reviewed papers related to conferences that have been organized under the same title and held every five years since 2008 to bring together the semigroup community and to celebrate consecutive birthdays (75th, 80th, and 85th, respectively) of Prof. Jan Kisyski. The previous volume reflects, to some degree, the second edition of the conference which took place in Bdlewo, Poland, in October 2013. The present volume is devoted to its third edition in Kazimierz Dolny, Poland, in October 2018.

Since the semigroup history does not change as quickly as the history of some other events, most of what we wrote in the preface to the previous volume is still correct today, and thus we will take the freedom of incorporating parts of it here. The foundations of the theory of semigroups of operators can be traced back to the formulation of the Cauchy equation,

and the work of G. Peano and his student M. Gramegna who, at the turn of the nineteenth and twentieth century, derived formulae for the solutions of, respectively, finite and infinite dimensional linear systems of differential equations in terms of exponential functions of a bounded linear operator defining the right-hand side of the system. Later, in the first half of the twentieth century, a formalization of the view, expressed by A. Hadamard, that an autonomous deterministic system should be described by a one-parameter semigroup of transformations, provided a more general background for the development of the theory of semigroups designed as a functional analytic language of partial differential equations. However, the concept soon also proved to be an important tool in stochastic processes, where mathematicians like W. Feller were instrumental in developing the foundations of the theory.

It can be safely said that the theory of semigroups, as a part of functional analysis, reached its maturity in the fourth and fifth decades of the previous century when the major generation theorems were established thanks to the work of K. Yosida, E. Hille, R. S. Phillips, I. Miyadera, and W. Feller. The state of the theory was summarised in the famous book Functional Analysis and Semi-Groups by E. Hille and R. S. Phillips, which firmly placed semigroups in the domain of functional analysis. It is interesting to note that the first book under that title (from which the famous quote: I hail a semi-group when I see one and I seem to see them everywhere! Friends have observed, however, that there are mathematical objects which are not semi-groups originated), published in 1948, was written only by E. Hille and was just 285 pages long. Such rapid was the advance of the theory in the next few years that a revised version, written together with R. S. Philips in 1955, grew to 808 pages. It has continued to be a basic reference in the field till now and possibly anybody who dares to read all 800 pages of it there will still find many challenging and generally unknown results.

Since then, semigroup theory not only has been rapidly developing as an independent field of research, posing new and fascinating questions but it also has become an indispensable tool and language for applications ranging from the classical ones such as partial differential equations and stochastic processes to less standard such as integro-differential and functional-differential equations, quantum mechanics, population biology, or control theory. Furthermore, though inherently linear and autonomous, semigroups became a cornerstone in the analysis of both nonlinear and nonautonomous evolutionary phenomena.