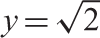Contents
List of Figures
List of Tabless
Guide
Pagebreaks of the print version

Intelligent Robotics and Autonomous Agents
Edited by Ronald C. Arkin
A complete list of the books in the Intelligent Robotics and Autonomous Agents series appears at the back of this book.
The Developmental Organization of Robot Behavior
Roderic Grupen
The MIT Press
Cambridge, Massachusetts
London, England
2023 Roderic Grupen
All rights reserved. No part of this book may be reproduced in any form by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher.
The MIT Press would like to thank the anonymous peer reviewers who provided comments on drafts of this book. The generous work of academic experts is essential for establishing the authority and quality of our publications. We acknowledge with gratitude the contributions of these otherwise uncredited readers.
Library of Congress Cataloging-in-Publication Data
Names: Grupen, Roderic A., author.
Title: The developmental organization of robot behavior / Roderic A. Grupen, Laboratory for Perceptual Robotics Department of Computer Science, University of Massachusetts Amherst.
Description: Cambridge: The MIT Press, [2023] | Series: Intelligent robotics and autonomous agents series | Includes bibliographical references and index.
Identifiers: LCCN 2020033973 | ISBN 9780262073004 (hardcover)
Subjects: LCSH: Autonomous robots. | Cooperating objects (Computer systems) | Machine learning.
Classification: LCC TJ211.495.G77 2021 | DDC 629.8/92dc23
LC record available at https://lccn.loc.gov/2020033973
d_r0
Contents
List of Figures
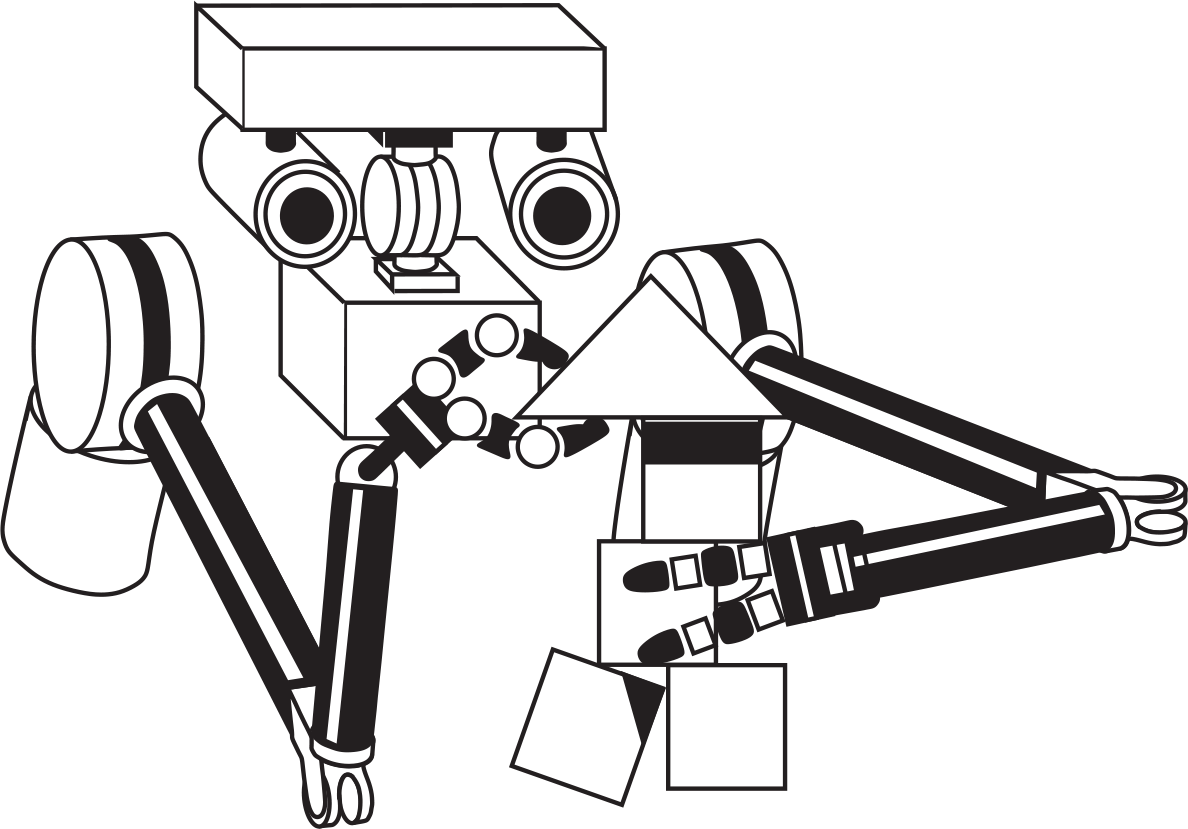
A mobile manipulator concept for exploring robotics, control, signal processing, learning, and behavior.
]).
].)
])
])
])
])
])
. The Huxley model combining active and passive muscle dynamics
. A charge q moving along a conductor at velocity v through a magnetic field, B , from north to south magnetic poles
. Moving electric charges create a torque on the coil due to the Lorentz force
. Faradays law describes how electrical current is generated in response to a mechanical input energy
. The iron core DC motor
. Electromechanical model of the DC motor
. Plot colors and the corresponding vertical axes illustrate a family of performance curves relating motor speed, current, power, and efficiency to the torque generated by a DC motor
. The compound load of the motor-gearhead combination
. The hydraulic servo valve directs high pressure hydraulic fluid from a reservoir to drive a piston: (left) flow for extending the linear actuator; (right) flow for retracting the actuator.
. The Sarcos GRLA (General Large Robot Arm)
. The jet-pipe servo valve for controlling pneumatic actuators
. The Utah/MIT dextrous hand with polymeric tendons and analog control box
. The operation of an air muscle
)
])
])
. The mechanisms that contribute to the quadriceps femoris stretch reflex (L4) in response to the tapping of the patellar tendon
. The spring-mass-damper (SMD) system
. The free body diagram of the SMD system
. A trajectory of an asymptotically stable harmonic oscillator on a bowl-shaped Lyapunov function (left) and the top-view projection on the phase plane (right)
. Qualitative state space trajectories of the harmonic oscillator
. The 1 DOF revolute (1R) mechanism is the inertial object in a PD control process with reference ref
. The transfer function for the generic harmonic oscillator in the form of a SISO filter
. Series and parallel composition of transfer functions and the closed-loop transfer function (CLTF)
. The musculature for the eyes lateral (pan) degree of freedom
. A control model for the 1-DOF oculomotor system consists of active and passive elements
. A sequence of compositions yields the closed-loop transfer function for the PD controlled, oculomotor system
. The unit step reference input
as a function of (K =1.0 [Nm/rad], I =2.0 [kgm2]) given boundary conditions 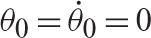 and =1.0 [rad]
and =1.0 [rad]
. The response of the second-order PD position controller to cos(t) input function, where is the driving frequency for various values of
. Coordinate frames commonly used to specify robot tasks
. The kinematic definitions and intermediate coordinate frames used to define Roger
. Two coordinate frames related through a pure translation
. Two coordinate frames related through a pure rotation
. Projecting 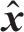 C onto the x-y plane of frame B
C onto the x-y plane of frame B
. Two coordinate frames related through a rotation and a translation
. The planar 2R manipulator
. The reachable workspace for the planar 2R robot
. The Unimate PUMA 560
. The human shoulder, arm, and wrist. Three intersecting revolute axes in the wrist create an approximately spherical wrist joint important for brachiation in human ancestors
. A geometric construction for simplifying the inverse kinematic solution
. The complete inverse kinematic mapping for the planar 2R manipulator
. The pinhole camera geometry
. Top view of a 2D stereo geometry where depth is encoded exclusively in stereo disparity
. The binocular imaging geometry with independently panning cameras. On the right, the stereo geometry is defined in terms of parameter = +, the sum of the eye configuration, , and the angular offset from the fovea,
. Multi-sensor models of space and hand-eye coordination. This illustration uses a different coordinate system than other Roger examples, and arms/hands have been removed from images for clarity.
. The Jacobian of the 2R manipulator transforms sets of executable velocities in configuration space from posture (1, 2) into sets of achievable velocities in Cartesian space from endpoint position (x, y)
. Singularities in the 2R manipulator
. The 2D planar manipulator and a specific endpoint velocity command
. The velocity ellipsoid in terms of the eigenvalues and eigenvectors of JJ T for the planar 2R manipulator
. The manipulator conditioning ellipsoids JJ T for Rogers 2R manipulator
. Triangulation parameters for Rogers stereo system
. Scaled localizability ellipsoids for Rogers stereo geometry
. Redundant solutions for the planar 3R manipulator at x=1, 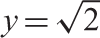
. Internal motions along the self-motion manifold of the planar 3R manipulator with l1 =l2 =l3 =1 and fixed endpoint position at x=1.0, 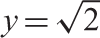
. A palm view of the right hand shows the fingers intrinsic iterossei muscles containing as many as 120 muscle spindles per gram of tissue










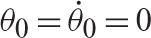 and =1.0 [rad]
and =1.0 [rad]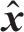 C onto the x-y plane of frame B
C onto the x-y plane of frame B