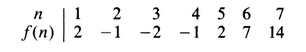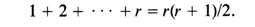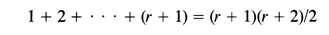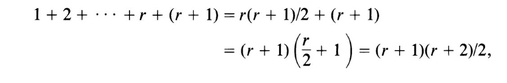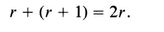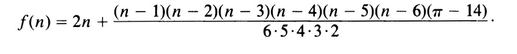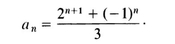Underwood Dudley - Elementary number theory

In the text, the method of proof by mathematical induction is used several times. The purpose of this section is to recall what the method is, show some examples of how it operates, and give some problems for practice.

Mathematics is notoriously a deductive art: starting with a collection of postulates, theorems are deduced by following the laws of logic. That is the way it is presented in print, but that is not the way that new mathematics is discovered. It is difficult to sit down and think, I will now deduce, and deduce anything worthwhile. The goal must be in sight: you must suspect that a theorem is true, and then deduce it from what you know. The theorem you suspect is true must come from somewhere. Just as in the other sciences, a new result can come at any time, the mysterious product of inspiration, inspection, subconscious rumination, revelation, or a correct guess.

* Exercise 1 . Guess what f ( n ) is from the following data:

* Exercise 2 . Guess what f ( n ) is from

* Exercise 3 (optional). Guess a theorem about f ( n ):

Since number theory is largely concerned with the positive integers, some of its theorems are of the form, Such-and-such is true for all positive integers n. Propositions like this can often be proved by mathernatical induction (or induction for short-we will not be concerned with any other kind). This method of proof is based on the following property of positive integers:

If a set of integers contains 1, and

(1) if it contains r + 1 whenever it contains r, then the set contains all the positive integers.

This property is so fundamental that it is usually taken as a nonprov-able postulate about the positive integers. It is applied when we want to show that a proposition P ( n ) about the positive integer n is true for all n , n = 1, 2, .... Examples of such propositions are

P 1( n ): n 2 + 3 n + 2 > ( n + 1)2 - 5.

P 2( n ): n ( n + 1)( n + 2) is divisible by 6.

P 3( n ): f ( x 1 + x 2 + + x n ) f ( x 1) + f ( x 2) + + f ( x n ) .

Let S denote the set of positive integers for which P(n) is true. If we can show that 1 is in S and that if r is in S , then r + 1 is in S , then (1) says that all positive integers are in S . Rephrasing this, we get the induction principle:

If P (1) is true, and

if the truth of P ( r ) implies the truth of P ( r + 1),

then P ( n ) is true for all n, n = 1, 2, ....

There is no necessity for an induction to start with 1; we could start with 2, 3, 17, or -12. For example, if P (3) is true and if the truth of P ( r ) implies the truth of P ( r + 1), then P ( n ) is true for n = 3, 4, ....

* Exercise 4 . Fill in the blank: if P (2) is true, and if the truth of P ( r ) implies the truth of P ( r + 2), then P ( n ) is true for ___.

To illustrate a proof by induction, we will take a well known example. Let P ( n ) be the statement

1 + 2 + + n = n ( n + 1)/2.

We will prove by induction that P ( n ) is true for all positive integers n.

* Exercise 5 . What is P (1)? Is it true?

Suppose that P ( r ) is true; that is, suppose that

(2)

We wish to deduce that P ( r + 1) is true. That is, we want to show that

(3)

follows from (2). If we add r + 1 to both sides of (2), we get

which is (3). Hence both parts of the induction principle have been verified, and it follows that P ( n ) is true for all positive integers n.

In any proof by induction, we must not forget to show that P (1) is true. Even if we show that the truth of P ( r ) implies the truth of P ( r + 1), if P (1) is not true, then we cannot conclude that P ( n ) is true for any n. For example, let P ( n ) be

n + ( n + 1) = 2 n .

Suppose that P ( r ) is true. That is, we assume that

(4)

Using this, we have

( r + 1) + ( r + 2) = r + ( r + 1) + 2 = 2 r + 2 = 2( r + 1),

so P ( r + 1) is true. So, if P (1) were true, it would follow that P ( n ) is true for all positive integers n . Since P (1) is not true, we cannot so conclude. In fact, P ( n ) is false for all n .

It should go without saying that in any proof by induction, we must verify that the truth of P ( r ) implies the truth of P ( r + 1). For example, from the table

we cannot conclude that f ( n ) = 2 n for all n . In fact, f (7) = , because the function that I had in mind when constructing the table was

Another form of the induction principle is sometimes used:

If P (1) is true, and

if the truth of P ( k ) for 1 k r implies the truth of P ( r + 1),

then P ( n ) is true for all n , n = 1, 2, ....

This is valid because of the corresponding property of integers: if a set of integers contains 1, and contains r + 1 whenever it contains 1, 2, ... , r , then it contains all positive integers.