Joseph Breuer - Introduction to the Theory of Sets

Introduction to the

THEORY OF SETS

Introduction to the

THEORY OF SETS

Joseph Breuer

Translated by

Howard F. Fehr

DOVER PUBLICATIONS, INC., MINEOLA, NEW YORK

Bibliographical Note

This Dover edition, first published in 2006, is an unabridged republication of the work originally published by Prentice-Hall, Inc., Englewood Cliffs, New Jersey, in 1958.

International Standard Book Number: eISBN 13: 978-0-486-15487-9

Manufactured in the United States of America

Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y 11501

PREFACE

Today questions concerning the foundations of mathematics are again receiving considerable attention. In particular, set theory has become an important area of investigation because of the way in which it seems to permeate so much of contemporary mathematical thought. The subject of set theory may be considered as originating with Georg Cantor, who attempted to organize concepts on collections of objects into a structure which could serve as a basis for a mathematical theory of the infinite. The infinite, in this sense, is not the potential, unattainable type used in the theory of limits, but the actual or proper type conceived as a completely determined object lying beyond all finite magnitudes. How well Cantor succeeded is easily recognized in the extension of the theory from the original naive, plausible approach to the present-day abstract, axiomatic development which has become the basis of structure in algebra, geometry, and analysis.

In the English language there exists today only scattered fragmentary or advanced treatises on the subject. There is now a need for a treatment of set theory in English, from a less than abstract axiomatic approach, sufficiently elementary to serve as an introduction to the subject for college and high school instructors, college students, and interested laymen. This book meets that need. A naive approach, which depends upon observation of the concrete world for its development and meaning, is a natural way to introduce the subject, and this procedure is used in the following exposition. Little by little, certain properties and principles are developed, which in turn are used to prove further theorems concerning sets as collections of abstract entities. Thus one is led from concrete finite sets, to cardinal numbers, to infinite cardinals, and thence to ordinals via the use of ordinal-types.

Abstract set theory based on an axiomatic system is not treated here. For those who care to pursue the subject further, the appended bibliography provides directed study. The axiom of choice and its relation to the theorem of well-ordering have had tremendous effect on the whole development of set theory, but these are matters of concern to the mathematician rather than to the neophyte. This translation is offered with the hope that it will provide for the reader sufficient background and impelling interest for further study.

Howard F. Fekr

CONTENTS

INTRODUCTION

Geometry and analysis, differential and integral calculus deal continually, even though perhaps in disguised expression, with infinite sets. Thus wrote F. Hausdorff (1914) in his Fundamentals of the Theory of Sets. To attain a genuine understanding and mastery of these various branches of mathematics requires a knowledge of their common foundation, namely, the theory of sets.

We may ask, what are the things with which mathematics concerns itself? They are, in every case, sets of numbers or sets of pointsgenerally infinite sets, that is, sets which contain an infinite number of things.

The reader may question the idea of approaching the infinite by means of mathematical analysis, thus bringing it under the control of mathematical laws and formulas. But this approach is the essence of the theory of sets. For this purpose, our concept of the infinite must be separated from vague emotional ideas and from the infinite of nonmathematical realms (the infinite of metaphysics).

Before Cantors time, the infinite in mathematics was an obscure and unpredictable area. Even Gauss, in 1831, was of the opinion that: The infinite is only a manner of speaking in that one actually talks of limits which certain ratios approach as closely as desired, while other ratios are permitted to grow larger without bounds. Gauss, himself, rejected the use of an infinite number, as something which is never permitted in mathematics. He recognized the infinite only in the sense of a process of becoming infinite in the limit: .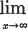

recognized that the infinite in mathematics was replete with paradoxes (contradictions) obstructing arithmetical treatment of the subject. It was Cantor, however, who taught us how to calculate with the infinite through his introduction of clearly determined and sharply differentiated infinite numbers, with well-defined operations upon them: It concerned an extension; that is, a continuation of the sequence of real integers beyond the infinite. As daring as this might seem, I not only express the hope, but also the firm conviction that, in time, this extension will come to be looked upon as thoroughly simple, acceptable, and natural.

After a ten-year delay, when he had come to recognize that his concepts were indispensable to the further development of mathematics, Cantor decided to publish his creation. In this work, he generalized the laws and rules applied to finite numbers so that they would extend beyond the domain of these numbers. He explained how one could compute with infinite sets, using the same methods that are applied to finite sets. With a few clearly defined concepts such as order (going back to Dedekind), power or cardinal number, denumerability, etc., he raised the theory of sets to a science which no longer contained fundamental barriers between the finite and the infiniteone that made the infinite understandable.

Today we know that Cantor, as Hilbert has said, thereby created one of the most fertile and powerful branches of mathematics; a paradise from which no one can drive us out. The theory of sets stands as one of the boldest and most beautiful creations of the human mind; its construction of concepts and its methods of proof have reanimated and revitalized all branches of mathematical study. The theory of sets, indeed, is the most impressive example of the validity of Cantors statement that, The essence of mathematics lies in its freedom.

Mathematics exercises its freedom in asking questions. Who has not at some time posed questions of the following kind?

Are there more whole numbers than there are even numbers?

Does an unbounded straight line contain more points than a line segment?

Does a plane contain fewer points than space?

Are the rational points densely situated on the number scale?

In particular, what do + 1, and 3, and 2 denote?

People refrained from discussing these questions publicly since such inquiries seemed naive or stupid and, above all, because they appeared to have no answer. However, the theory of sets gives clear answers possessing mathematical precision to all these questions, when the questions are properly phrased.

The foundation of the general theory of sets has now been established for over half a century. To understand it calls for scarcely any prerequisite technical knowledge. All that is necessary is an interest in establishing the infinitely large and a patience for grasping somewhat difficult concepts. Even though the theory of sets starts in the intuitive-concrete, it nevertheless climbs to a very high degree of abstraction.

This book is an introduction to the theory of sets. In the first few pages the fundamental concepts will be developed through the use of well-known finite sets. Although the theory of finite sets is nothing else than mere arithmetic and permutations and combinations, yet it helps to provide the terminology and symbolism of set theory. These concepts will provide the basis for the subsequent treatment of the infinite sets. The general theory of sets ends with a discussion of ordered sets. A few important theorems on point sets are appended in a supplement. Definitions that produce paradoxes are merely alluded to in the concluding paragraphs.