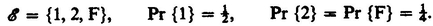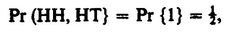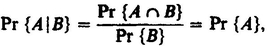This appendix contains a hasty survey of the probability theory needed in the text. It can be used as a review for those who have had some probability theory. For those who have not had any, it can be used as an adjunct to lectures on the subject.
A.1. THE NOTION OF PROBABILITY
If I toss a fair coin, what are the chances that it will come up heads? We expect to see 50% heads in the long run and so write
This is read, The probability of the event the coin lands heads up after this toss equals 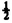 ; however, we shorten it to, The probability of heads equals
; however, we shorten it to, The probability of heads equals 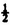 .
.
What happens when we dont know the probability from a priori considerations? For example, what is the probability that a newborn baby will be a boy? We need to say very carefully what we mean. The fraction of newborn children who have been males in recent years has been 0.514 in the United States. Therefore we could say that the probability of a male child is 0.514 if the expectant mother is American. However, if you told me that she is a black American, I would recommend changing the probability to 0.506, since this is the observed fraction when the mother is a black American. Whats going on? The population Im looking at has changed from all babies recently born to American women to all babies recently born to black American women. Note that both these populations are drawn from the past; as in all of science Im assuming that the future will resemble the past. Although these considerations are essential for applications, they should not enter into the theoretical framework of probability theory to which we now turn our attention. The problem of estimating probabilities, to which Ive alluded above, comes up again in the last paragraph of Section A.5.
DEFINITION . Let be a finite set and let Pr be a function from to the nonnegative real numbers such that
(Note the braces instead of parentheses for the function.) We call the event set, the elements of the simple events, and Pr { e } the probability of the simple event e.
As an illustration, consider tossing a fair coin twice. The outcomes can be denoted by the obvious notation HH, HT, TH, and TT. We can think of these as simple events and write
= {HH, HT, TH, TT}.
Also, 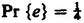 for each e . As another illustration, suppose that we toss the coin until a head occurs or until we have completed two tosses. Then the simple events can be denoted by 1, 2, and Fmeaning a head at the first toss, a head at the second toss, and a failure to obtain a head. These correspond, respectively, to H, TH, and TT in the previous notation. We have
for each e . As another illustration, suppose that we toss the coin until a head occurs or until we have completed two tosses. Then the simple events can be denoted by 1, 2, and Fmeaning a head at the first toss, a head at the second toss, and a failure to obtain a head. These correspond, respectively, to H, TH, and TT in the previous notation. We have
Note that the simple events in both examples are mutually exclusive and exhaustive; that is, exactly one occurs. This is the case in all interpretations of simple events.
If we had tossed a coin twice in the last example, we could think of event 1 as being the occurrence of either of the two simple events, HH and HT. We would write this as 1 = {HH, TT}. Thus we would write
and read the left side as the probability of either HH or HT occurring. More generally,
DEFINITION. For any subset S of we define Pr { S } to be the sum of Pr { e } over all e S and refer to it as the probability that a simple event in S will occur or, briefly, the probability that S will occur.
We can estimate Pr { S } by sampling from in such a way that each elementary event e is chosen with probability Pr { e }. (For the examples given above, our sampling can be accomplished by repeatedly tossing the coin.) If N S of the elementary events in such a sample of size N lie in S, then N S /N is an estimate for Pr { S }. This is the idea behind Monte Carlo simulation. Well find it convenient to use the abbreviation Pr {statement} for Pr { S }, where S is the set of all e such that the statement is true if e S occurs and false if e S occurs. For example, in the two tosses of a fair coin, Pr { 1 head} stands for the probability of the set { HT, TH, HH } .
We need two other concepts. After defining them, Ill discuss them briefly.
DEFINITION . The conditional probability of A given B is defined to be Pr { A B }/Pr { B } and is denoted by Pr { A | B }. The sets of events A and B are called independent if
Pr { A B } = Pr { A } Pr { B }.
Conditional probability is interpreted as the probability that e A given that e B . We can think of this as restricting our attention to B: If we estimate probability by counting, as described earlier, we will estimate the probability that an event in B lies in A by N AB / NB . Since this equals ( N AB / N )/( N B /N ), we see that the definition of conditional probability agrees with the notion of restricting our attention to the events in B.
We can think of independence as follows. Knowing that e B gives no information about whether or not e A, since
by the definitions of conditional probability and independence. By symmetry, the roles of A and B can be interchanged.
PROBLEMS
- Prove that Pr { A B } = Pr { A } + Pr { B } Pr { A B }.
- Two dice are thrown. All that matters is the sum of the two values. Formulate this in a probabilistic framework.
- We are looking at U.S. coins minted in the 1960s. Our interest is in denomination, date, and mint. Discuss some things we could consider and cast them all in the appropriate terminology, assuming that a simple event corresponds to observing a single coin. To begin with, what is ? Does it help to know the number of each type of coin that was minted? Why?











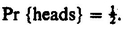
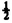 ; however, we shorten it to, The probability of heads equals
; however, we shorten it to, The probability of heads equals 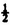 .
.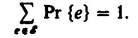
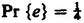 for each e . As another illustration, suppose that we toss the coin until a head occurs or until we have completed two tosses. Then the simple events can be denoted by 1, 2, and Fmeaning a head at the first toss, a head at the second toss, and a failure to obtain a head. These correspond, respectively, to H, TH, and TT in the previous notation. We have
for each e . As another illustration, suppose that we toss the coin until a head occurs or until we have completed two tosses. Then the simple events can be denoted by 1, 2, and Fmeaning a head at the first toss, a head at the second toss, and a failure to obtain a head. These correspond, respectively, to H, TH, and TT in the previous notation. We have