Goudon - Mathematics for modeling and scientific computing

1. 1 Ordinary Differential Equations
2. 2 Numerical Simulation of Stationary Partial Differential Equations: Elliptic Problems
3. 3 Numerical Simulations of Partial Differential Equations: Time-dependent Problems

First published 2016 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc.

Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:

ISTE Ltd
27-37 St Georges Road
London SW19 4EU
UK
www.iste.co.uk

John Wiley & Sons, Inc.
111 River Street
Hoboken, NJ 07030
USA
www.wiley.com

ISTE Ltd 2016

The rights of Thierry Goudon to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988.

Library of Congress Control Number: 2016949851

British Library Cataloguing-in-Publication Data
A CIP record for this book is available from the British Library
ISBN 978-1-84821-988-5

Early he rose, far into the night he would wait, To count,
to cast up, and to calculate, Casting up, counting,
calculating still, For new mistakes for ever met his view.
Jean de La Fontaine

(The Money-Hoarder and Monkey, Book XII, Fable 3).

This book was inspired by a collection of courses of varied natures and at different levels, all of which focused on different aspects of scientific computing. Therefore, it owes much to the motivation of students from the universities of Nice and Lille, and the Ecole Normale Suprieure. The writing style adopted in this book is based on my experience as a longtime member of the jury for the agrgation evaluations, particularly in the modeling examination. In fact, a substantial part of the examples on the implementation of numerical techniques was drawn directly from the texts made public by the evaluations jury (see http://agreg.org), and a part of this course was the foundation for a series of lectures given to students preparing for the Moroccan agrgation evaluations. However, some themes explored in this book go well beyond the scope of the evaluations. They include, for example, the rather advanced development of Hamiltonian problems, the fine-grained distinction between the finite-difference method and the finite-volume method, and the discussion of nonlinear hyperbolic problems. The latter topic partially follows a course given at the IFCAM (Indo-French Centre for Applied Mathematics) in Bangalore. A relatively sophisticated set of tools is developed on this topic: this heightened level can be explained by the fact that the questions it explores are of great practical importance. It provides a relevant introduction for those who might want to learn more, and it prepares them for reading more advanced and specialized works.

Numerical analysis and scientific calculus courses are often considered a little scary. This fear is often due to the fact that the subject can be difficult on several counts:

1. problems of interest are very strongly motivated by their potential applications (for example, in physics, biology, engineering, finance). Therefore, it is impossible to restrict the discussion strictly to the field of mathematics, and the intuitions motivating the math are strongly guided by the specificities of its applications. As a result, the subject requires a certain degree of scientific familiarity that goes beyond mere technical dexterity.
2. Numerical analysis uses a very ample technical background. This is a subject that we cannot address by utilizing a small and previously delimited set of tools. Rather, we must draw from different areas of mathematics, sometimes in rather unexpected ways, for example by using linear algebra to analyze the behavior of numerical approximations to differential equations. However, this somewhat roundabout way of finding answers is what makes the subject so exciting.
3. Finally, it is often difficult to produce categorical statements and conclusions. For example, although it can be shown that several numerical schemes produce an approximate solution that converges towards the solution of the problem of interest (when the numerical parameters are sufficiently small), in practice, some methods are more suitable than others, according to qualitative criteria that are not always easy to formalize. Similarly, the choice of method may depend on the criteria that are considered most important for the target application context. Many questions do not have definite, clear-cut answers. The answer to the question how should we approach this problem? is often it depends: numerically simulating a physical phenomenon through calculations performed by a computer is a real, delicate and nuanced art. This art must be based on strong technical mastery of mathematical tools and deep understanding of the underlying physical phenomena they study.

The aim of this book is to fully address these challenges and, by design, to mix everything up. Therefore, the book will include many classical results from analysis and algebra, details for certain equation resolution algorithms, examples from science and technology, and numerical illustrations. Some theoretical tools will be introduced by studying an application example, even if it means repurposing it for an entirely different field. Nevertheless, the book does follow a certain structure, which is organized into three main sections, focused on numerical solutions to (ordinary and partial) differential equations. The first chapter addresses the solution of ordinary differential equations, with a very broad overview of its essential theoretical basis (for example, CauchyLipschitz, qualitative analysis, linear problems). This chapter details the analysis of classical schemes (explicit and implicit Euler methods), and distinguishes various concepts of stability, which are more or less relevant depending on the context. This set of concepts is illustrated by a series of examples, which are motivated mostly by the description of biological systems. A large section, with fairly substantial technical content, is devoted to the particular case of Hamiltonian systems. The second chapter deals with numerical solutions to elliptic boundary value problems, once again with a detailed exploration of basic functional analysis tools. 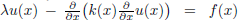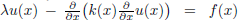Although the purpose is mostly restricted to the one-dimensional framework and to the model problem on ]0, 1[ with homogeneous Dirichlet conditions, different discretization families are distinguished: finite differences, finite volumes, finite element and spectral methods. Techniques related to optimization are also presented through the simulation of complex problems such as BoltzmannPoisson equations, load optimization and Stokes problem. The last chapter deals with evolutionary partial differential equations, again addressing only the one-dimensional case. Questions of stability and consistency are addressed in this chapter, first for the heat equation and then for hyperbolic problems. The transport and wave equations can be considered classics. In contrast, discussion of nonlinear equations, scalars or systems with the simulations of Euler equations for gas dynamics as a final target, leads to more advanced topics. The book does not contain exercise problems. However, readers are invited to carry out the simulations illustrated in the book on their own. This work of numerical experimentation will allow readers to develop an intuition of the mathematical phenomena and notions it presents by playing with numerical and modeling parameters, which will lead to a complete understanding of the subject.