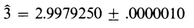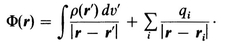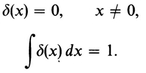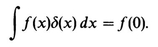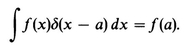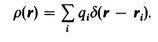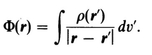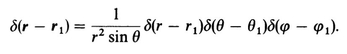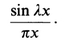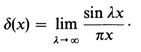Eyges - The Classical Electromagnetic Field.
Here you can read online Eyges - The Classical Electromagnetic Field. full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Newburyport, year: 2012, publisher: Dover Publications, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
The Classical Electromagnetic Field.: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "The Classical Electromagnetic Field." wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
3.8 DIPOLE DISTRIBUTIONS-INTERIOR FIELDSPROBLEMS; REFERENCES; 4 - BOUNDARY VALUE PROBLEMS WITH CONDUCTORS; 4.1 THE PHYSICS OF CONDUCTORS IN FIELDS; 4.2 HOMOGENEOUS AND INHOMOGENEOUS PROBLEMS; 4.3 A UNIQUENESS THEOREM; 4.4 METHOD OF IMAGES; 4.5 LAPLACES EQUATION AND SUPERPOSITION OF ELEMENTARY SOLUTIONS; 4.6 COMPOSITE PROBLEMS; 4.7 INTEGRAL EQUATIONS; PROBLEMS; REFERENCES; 5 - GENERAL BOUNDARY VALUE PROBLEMS; 5.1 DIRICHLET AND NEUMANN PROBLEMS; 5.2 SUPERPOSITION OF ELEMENTARY SOLUTIONS; 5.3 GREENS THEOREM AND AN INTEGRAL IDENTITY FOR THE POTENTIAL.
5.4 A GENERALIZED INTEGRAL IDENTITY AND GREEN FUNCTIONS5.5 APPLICATION OF GREEN FUNCTIONS; 5.6 GENERAL PROPERTIES OF GREEN FUNCTIONS; PROBLEMS; REFERENCES; 6 - DIELECTRICS; 6.1 INTRODUCTION; 6.2 POLARIZATION CHARGE AND THE AVERAGE INTERNAL FIELD; 6.3 THE RELATION OF POLARIZATION TO THE APPLIED FIELD; 6.4 CAPACITORS AND THE DIELECTRIC CONSTANT; 6.5 BOUNDARY VALUE PROBLEMS WITH DIELECTRICS; 6.6 MACROSCOPIC AND MICROSCOPIC PROPERTIES; PROBLEMS; REFERENCES; 7 - THE MAGNETOSTATIC FIELD; 7.1 CURRENT AND RELATED CONCEPTS; 7.2 FORCES BETWEEN CONDUCTORS AND THE MAGNETOSTATIC FIELD B.
7.3 DIFFERENTIAL AND INTEGRAL PROPERTIES OF B7.4 THE MAGNETIC SCALAR POTENTIAL; 7.5 THE VECTOR POTENTIAL; PROBLEMS; REFERENCE; 8 - THE SUMMATION PROBLEM FOR STATIONARY CURRENTS; 8.1 INTRODUCTION; 8.2 INTEGRAL MAGNETIC SCALAR POTENTIAL; 8.3 DIFFERENTIAL MAGNETIC SCALAR POTENTIAL; 8.4 THE VECTOR POTENTIAL AND A MULTIPOLE EXPANSION; 8.5 EXTERNAL FIELD OF DIPOLAR MAGNETIC MATTER; PROBLEMS; REFERENCES; 9 - MAGNETIC MATERIALS AND BOUNDARY VALUE PROBLEMS; 9.1 INTRODUCTION; 9.2 AN AVERAGE INTERNAL FIELD; 9.3 A POSTULATE RELATING MEAN MAGNETIZATION AND THE APPLIED FIELD.
9.4 THEORY OF PERMEABLE MATTER IN AN APPLIED FIELD9.5 THE VECTOR H; 9.6 A BOUNDARY VALUE PROBLEM; PROBLEMS; REFERENCES; 10 - FORCE AND ENERGY IN STATIC FIELDS; 10.1 ENERGY OF ASSEMBLAGE OF CHARGE DISTRIBUTION; 10.2 ENERGY OF FORMATION OF CURRENT DISTRIBUTION; 10.3 RIGID CHARGE DISTRIBUTION IN APPLIED ELECTRIC FIELD; 10.4 RIGID CURRENT DISTRIBUTION IN APPLIED MAGNETIC FIELD; 10.5 FORCE ON CONDUCTORS; 10.6 DIELECTRIC MATTER IN APPLIED ELECTRIC FIELD; 10.7 PERMEABLE MATTER IN APPLIED MAGNETIC FIELD; PROBLEMS; REFERENCES; 11 - TIME-VARYING FIELDS; 11.1 INTRODUCTION.
11.2 FARADAYS LAW OF INDUCTION.
This excellent text covers a years course in advanced theoretical electromagnetism, first introducing theory, then its application. Topics include vectors D and H inside matter, conservation laws for energy, momentum, invariance, form invariance, covariance in special relativity, and more. Read more...
Eyges: author's other books
Who wrote The Classical Electromagnetic Field.? Find out the surname, the name of the author of the book and a list of all author's works by series.














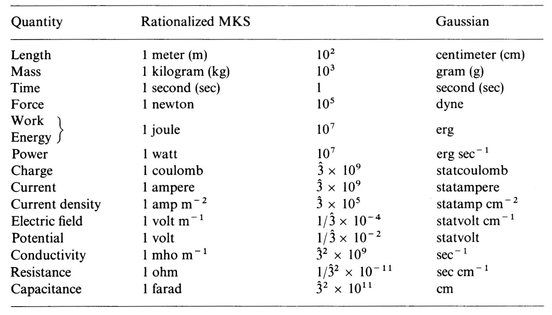
 MKS UNITS
MKS UNITS