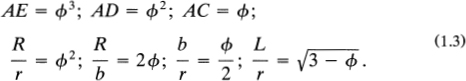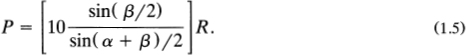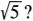Acknowledgments
Numerous people gave me considerable assistance during the period of preparation of this book. I am grateful to the following persons for their willingness to read various chapters of my manuscript: Philip J. Davis, J. Donald Fernie, Paulo Ribenboim, O. J. Sikes, Whitney Smith, and John P. Snyder.
Others aided in a substantial way by providing information dealing with all kinds of things. For this help, I would like to express appreciation to Teresita Barsana, Brian Bilbray, Roman Dannug, Bill Dillon, and Susan Harris.
As before, I express much gratitude to my editor, Trevor Lipscombe, and to many others at Princeton University Press, for their greatly appreciated efforts to turn my manuscript into a book.
It is impossible to list the many contributions my wife, Gunta, made to this endeavor. I thank her for all she has done. In my earlier book, her wise advice and cheerful help certainly improved the likelihood of a successful towing of that literary iceberg. This time, once again, her wise counsel and cheerful assistance surely strengthen the chances of a creditable race by her husband, a literary turtle.

Paradoxes, Perplexities & Mathematical Conundrums for the Serious Head Scratcher
Slicing Pizzas, Racing Turtles, and Further Adventures in Applied Mathematics, by Robert B. Banks
Chases and Escapes: The Mathematics of Pursuit and Evasion,
by Paul J. Nahin
Duelling Idiots and Other Probability Puzzlers,
by Paul J. Nahin
Across the Board: The Mathematics of Chessboard Problems,
by John J. Watkins
1
Broad Stripes and Bright Stars
These days we see much more of the flag of the United States than we ever did in the past. Old Glory flies over many more office buildings and business establishments than it did before. It is now seen far more extensively in parks and along streets and indeed in a great many programs and commercials on television.
With this greatly increased presence and awareness of the flag, there is understandable growing interest in learning more about numerous aspects of the U.S. flag, including its history and physical features and the customs and protocol associated with it.
There are a number of books that examine various topics concerning the flag of the United States. Representative are the publications of Smith (1975a) and Furlong and McCandless (1981). On the world scene, many references are available dealing with the flags of all nations. For example, the books by Smith (1975b) and Crampton (1990) cover many subjects relating to flags of the world and to various other topics of vexillology: the art and science of flag study.
The Geometry of the Flag of the United States
With that brief introduction, we come directly to the point. The colors of the U.S. flag are red, white, and blue. Now, are you ready for the big question? What are the area percentages of red, white, and blue? That is, which of the three colors occupies the largest area of the flag and which color the smallest? It's a good question. Do you want to guess before we compute the answer?

FIG. 1.1
Flag of the United States.
The flag is shown in . Arbitrarily selecting the foot as the unit of linear measurement, here are some preliminary observations:
The total area of the flag is 1.0 1.9 = 1.9 ft2
The area of the union is 7/13 0.76 = 0.4092 ft2
The length of the seven upper stripes is 1.14 ft
The length of the six lower stripes is 1.9 ft
TABLE 1.1
Proportions and features of the U.S. flag
| Item | Quantity |
| Width of flag | 1.0 |
| Length of flag | 1.9 |
| Number of red stripes | 7 |
| Number of white stripes | 6 |
| Width of union | 7/13 |
| Length of union | 0.76 |
| Number of stars | 50 |
| Radius of a star | 0.0308 |
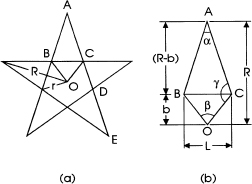
FIG. 1.2
Definition sketches for (a) pentagram and (b) pentagram kite.
The width of a stripe is 1/13 = 0.07692 ft
The problem of computing the red area is easy
The problem of computing the white and blue areas is not so easy because of the 50 white stars in an otherwise blue union
So, before we can obtain the final answer we have to look at stars
The Geometry of a Five-Pointed Star
A five-pointed star, commonly called a pentagram, is shown in . Its radius, R, is the radius of the circumscribing circle. The five-sided polygon within the star is called a pentagon; the radius of its circumscribing circle is r.
The section ABOC is removed from the pentagram of . Some geometry establishes that = 36, = 72, and = 126. Without much difficulty we obtain the expression
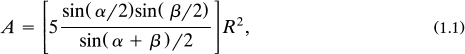
where A is the area of the pentagram. Substituting the values of and into this expression gives

For comparison, remember that the area of the circumscribing circle is R2 where, of course, = 3.14159. provides us with a simple formula to compute the area of a five-pointed star.
In elementary mathematical analysis we frequently run across the numerical quantity 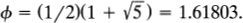 It is a very famous number in mathematics. It is called the golden number or divine proportion. Our pentagram is full of golden numbers. According to Huntley (1970), the following relationships prevail in based on unit length BC (i.e., one side of the pentagon):
It is a very famous number in mathematics. It is called the golden number or divine proportion. Our pentagram is full of golden numbers. According to Huntley (1970), the following relationships prevail in based on unit length BC (i.e., one side of the pentagon):
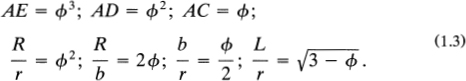
Utilizing these relationships, it can be established that the area of the regular pentagram can be expressed in terms of :

As we would expect from observing is 1.12257.
The perimeter of a pentagram is not difficult to determine. Using some geometry and trigonometry we obtain
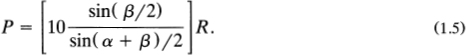
The bracketed quantity has the numerical value 7.2654. The length of the circumscribing circle is, of course, 2R.
Numerous other relationships could be established. For example, can you demonstrate that the ratio of the area of the five points of the pentagram to the area of the base pentagon is 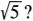
How Much Red, How Much White, How Much Blue?
We now have the information we need to answer the big question. From , the area of a single star is





















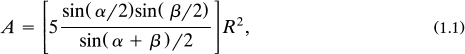

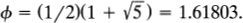 It is a very famous number in mathematics. It is called the golden number or divine proportion. Our pentagram is full of golden numbers. According to Huntley (1970), the following relationships prevail in based on unit length BC (i.e., one side of the pentagon):
It is a very famous number in mathematics. It is called the golden number or divine proportion. Our pentagram is full of golden numbers. According to Huntley (1970), the following relationships prevail in based on unit length BC (i.e., one side of the pentagon):