D. P. Craig - Molecular Quantum Electrodynamics
Here you can read online D. P. Craig - Molecular Quantum Electrodynamics full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2012, publisher: Dover Publications, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
Molecular Quantum Electrodynamics: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Molecular Quantum Electrodynamics" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
D. P. Craig: author's other books
Who wrote Molecular Quantum Electrodynamics? Find out the surname, the name of the author of the book and a list of all author's works by series.
Molecular Quantum Electrodynamics — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Molecular Quantum Electrodynamics" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
If A and B are two non-commuting operators, a c -number, then
(A1.1)
Proof
We first prove (A1.1) for the case when F(B) = Bn. (A1.1) then becomes,
(A1.2)
The proof of (A1.2) is immediate if the right-hand side of (A1.2) is written as
(A1.3)
and use is made of
(A1.4)
To prove the general identity (A1.1), it is assumed that F ( B ) admits a power series expansion in B :
(A1.5)
Then the left-hand side of (A 1.1 ) may be written
which on using (A1.2) becomes
(A1.6)
the right hand side of (A1.1).
If A and B are two non-commuting operators, then
(A1.7)
Proof
Let
(A1.8)
where is a real variable. Expanding F () as a power series in ,
(A1.9)
Clearly
(A1.10)
The first derivative is
(Al.11)
so that
(A1.12)
Using (A1.12)
(A1.13)
Hence,
(A1.14)
The result (A1.7) follows.
If A and B are non-commuting operators such that
(A1.15,)
then
(A1.16)
Proof
Let
(A1.17)
where is a real variabe. Then
(A1.18)
Usin Identity II (A1.7),
(A1.19)
Since ( A + B ) commutes with [ A,B ], they may be treated as commuting variables and (A1.18) may be integrated to give
(A1.20)
When = 1, (A1.20) becomes
(A1.21)
Therefore
(A1.22)
The second part of (A1.16) follows directly from (A1.22) by interchanging A and B in (A1.22)
Let the components of an nth rank tensor T with respect to a space-fixed frame be 
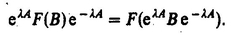
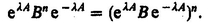
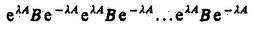
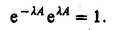
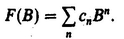
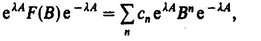
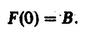
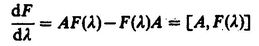
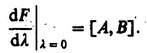
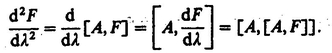
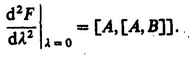
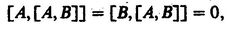
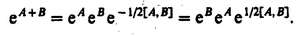
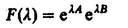
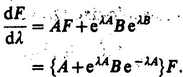
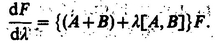
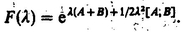
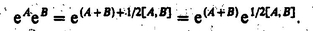
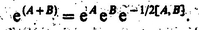
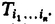If T refers to a molecular property, it is conveniently expressed with respect to a molecule-fixed frame through the relation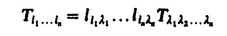
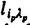(A2.1)
where 
is the cosine of the angle between the space-fixed axis ip and the molecule-fixed axis p. The Latin and Greek indices refer to space-fixed and molecule-fixed frames respectively. From (A2.1) it is seen that a rotational average of 
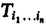requires the rotational average of the direction cosine product 
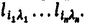By expressing the direction cosines in terms of Euler angles, the rotational average can be obtained from
(A2.2)
where , , and are the Euler angles relating the two frames. The trigonometric averaging procedure, though simple to use for tensors of low rank, becomes tedious for high n. A non-trigonometric procedure will now be outlined and results given for tensors up to rank 6.
Let us denote the rotational average 
Font size:
Interval:
Bookmark:
Similar books «Molecular Quantum Electrodynamics»
Look at similar books to Molecular Quantum Electrodynamics. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Molecular Quantum Electrodynamics and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.