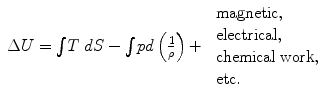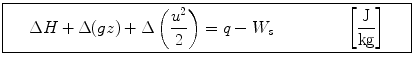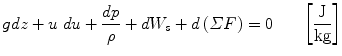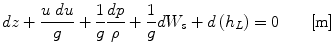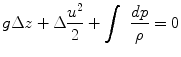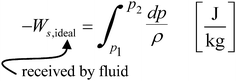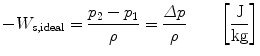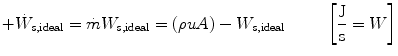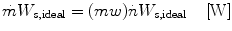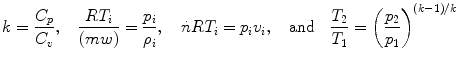Octave Levenspiel - Engineering Flow and Heat Exchange

Engineering Flow and Heat Exchange — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Engineering Flow and Heat Exchange" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...85

Part I
Flow of Fluids and Mixtures

Although the first part of this little volume deals primarily with the flow of fluids and mixtures through pipes, it also considers the flow of fluids through packed beds and through swarms of suspended solids called fluidized solids, as well as the flow of single particles through fluids. The term fluids and mixtures includes all sorts of materials under a wide range of conditions, such as Newtonians (e.g., air, water, whiskey), non-Newtonians (e.g., peanut butter, toothpaste), gases approaching the speed of sound, and gas flow under high vacuum where collisions between molecules are rare.

Chapter then take up the different kinds of flow.

Springer Science+Business Media New York 2014

Octave Levenspiel Engineering Flow and Heat Exchange 10.1007/978-1-4899-7454-9_1

1. Basic Equations for Flowing Streams

Octave Levenspiel 1

(1)

Department of Chemical Engineering, Oregon State University, Corvallis, OR, USA

1.1 Total Energy Balance

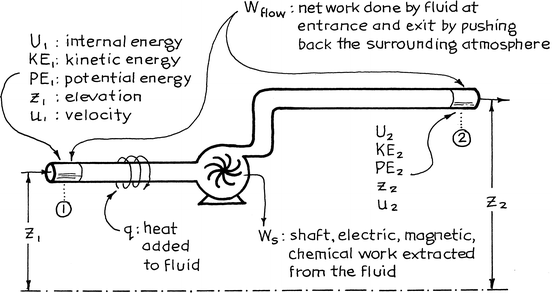
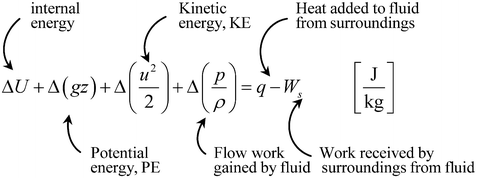
Consider the energy interactions as a stream of material passes in steady flow between points 1 and 2 of a piping system, as shown in Fig.. From the first law of thermodynamics, we have for each unit mass of flowing fluid:

Fig. 1.1

Energy aspects of a single-stream piping system

(1.1)

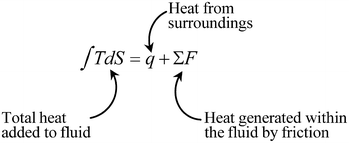
Consider the internal energy term in the above expression. From the second law of thermodynamics,

(1.2)

The T dS term accounts for both heat and frictional effects. Thus, in the ideal situation where there is no degradation of mechanical energy (no frictional loss, turbulence, etc.):

On the other hand, in situations where there is degradation (frictional losses),

(1.3)

Noting that H = U +( p/ ), we can rewrite equation () as

(1.4)

This is the first law of thermodynamics in its usual and useful form for steady-flow single-stream systems.

[ Authors Note : g c is a conversion factor, to be used with American engineering units. In SI units, g c is unity and drops from all equations. Since this book uses SI units throughout, g c is dropped in the text and problems.]

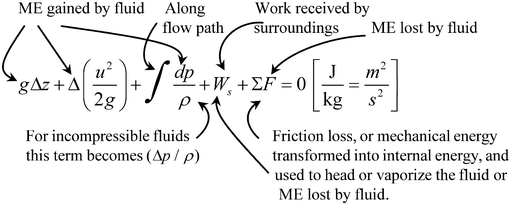
1.2 Mechanical Energy Balance

For each kilogram of real flowing fluid, with its unavoidable frictional effects, with no unusual work effects (magnetic, electrical, surface, or chemical), and with constant value of g , equations () combined give the so-called mechanical energy balance.

(1.5a)

Multiplying by 1/ g gives, in alternative form,

(1.5b)

In differential form these equations are

(1.6a)

and

(1.6b)

These equations, in fact, represent not a balance, but a loss of mechanical energy (the transformation into internal energy because of friction) as the fluid flows down the piping system. In the special case where the fluid does no work on the surroundings (W=0) and where the frictional effects are so minor that they can be completely ignored (F=0), the mechanical energy balance reduces to

(1.7)

which is called the Bernoulli equation.

The mechanical energy balance, equations (), is the starting point for finding work effects in flowing fluidspressure drop, pumping power, limiting velocities, and so on. We apply these expressions to all types of fluids and mixtures.

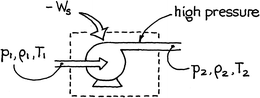
1.3 Pumping Energy and Power: Ideal Case

Pumps, compressors, and blowers are the means for making fluids flow in pipes. The shaft work needed by the flowing fluid is found by writing the mechanical energy

balance about the device. In the ideal case where the kinetic and potential energy changes and frictional losses are negligible, equation () reduces to

(1.8)

For liquids and slurries , and T const, so the shaft work from the surroundings to the fluid is

(1.9)

Thus the work delivered by the fluid

(1.10)

Assuming ideal gas behavior and adiabatic reversible compression or expansion, the work received by each unit of flowing gas is

(1.11)

The power produced by the flowing gas is then

(1.12)

where

(1.13)

1.4 Pumping Energy and Power: Real Case Compression

For gases compare ideal adiabatic compression with the real situation with its frictional effects and heat interchange with the surroundings, both cases designed to take fluid from a low pressure p 1 to a higher pressure p 2 . The p-T diagram of Fig. shows the path taken by the fluid in these cases.

Next page

1234567...85

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Engineering Flow and Heat Exchange»

Look at similar books to Engineering Flow and Heat Exchange. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Ashwin Pajankar

GNU Octave by Example: A Fast and Practical Approach to Learning GNU Octave

Bejan

Heat Transfer: Evolution, Design and Performance

Muthukumar Palanisamy (editor)

Theoretical, Computational, and Experimental Solutions to Thermo-Fluid Systems: Select Proceedings of ICITFES 2020 (Lecture Notes in Mechanical Engineering)

Eissa Al-Safran

Applied Multiphase Flow in Pipes and Flow Assurance - Oil and Gas Production: Textbook 14

Muske

An Octave above Thunder

Atesmen

Case Studies in Fluid Mechanics with Sensitivities to Governing Variables

Christopher Gorse

A Dictionary of Construction, Surveying, and Civil Engineering

Abram S. Dorfman

Applications of Mathematical Heat Transfer and Fluid Flow Models in Engineering and Medicine

Janna

Engineering Heat Transfer

Sandeep Nagar

Introduction to Octave: For Engineers and Scientists

Mike X Cohen

Fundamentals of Time-Frequency Analyses in Matlab/Octave

József Tóth

Gravitational Systems of Groundwater Flow: Theory, Evaluation, Utilization

Discussion, reviews of the book Engineering Flow and Heat Exchange and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.