1. Introduction to Octave
1.1 Introduction to Numerical Computing
Modern times have seen an exponential growth in scientific knowledge. Computing devices have benefited the most from this increase in knowledge. They started with mechanical solutions, whereby lever- and pulley-based computers were used to perform complex calculations with progressively fewer interventions. But mechanical systems were notorious slow and inefficient and there were energy concerns too. When vacuum tube based transistors were invented, they were applied to this domain. Vacuum tube based computers entered the research labs of academia and industry alike. During WWII, they were used to run programs to crack enemy codes as well as to simulate various scenarios for designing weapons. This infused much needed money and talent in this area and, within few years, the overall efficiency of computing devices saw an amazing exponential increase.
Simulating a real-world phenomenon involves solving equations governing these issues. Numerical simulation involves defining the problem for a digital computer. This can be achieved in two ways:
Using a programming language and encoding every step used for numerical computation
Using a specialized software framework that presents a general framework to define a mathematical problem that the computer understands
Scientific computation was initially performed by the first method. Programming languages like FORTRAN, C, and C++ became very popular. Even today these languages, and recent ones like Python and Julia, are still widely used for this purpose. But during the same time, the need for a specialized numerical computing framework was also recognized. Using programming languages, you could make a generalized scheme for numerical computing in which you could define a scientific problem. One of the biggest advantages of such an approach is that you can define a lot of library functions that can be simply used as and when required, instead of each user writing them down each time for a different problem. Hence, over the period of time a number of software programs came into existence.
One of them was MATLAB , and it became very popular all over the world. It is sometimes called the language of engineering for the right reasons, since most engineering problems can be easily defined using it. Engineers can concentrate on defining a problem rather than writing efficient code (which they can simply pick from a library). Being commercial software, MATLAB comes with a price as well as with a restrictive license. With the introduction of open source licensing, there was a need for an open source alternative. This is where Octave came into being. This book presents usage of Octave as an effective alternative to MATLAB.
1.2 Analytical vs. Numerical Schemes
Analytical schemes to solve mathematical problems involve deriving equations describing a system using relationships between various parameters and then solving these equations by either using invented functions (mapping of variables from one domain to another) or inventing new functions that fit the purpose. On the other hand, a numerical scheme also requires describing the system using a relationship between various parameters and functions, but deriving a solution has a marked difference. This can be shown with a simple example.
Lets try to find a value of x that can satisfy the equation f ( x ) = x + 25. Finding an analytical solution involves the following steps:
x + 2 = 0
Add 2 to both sides
x = 2 is the answer
On the other hand, a numerical solution using the bisection method involves first guessing a value as a solution of the equation and then following the scheme as shown here:
Lets guess 3 as the answer
f (3) = 1 + 2 = 3 > 0 so lets guess f (3) = 3 + 2 = 1 < 0
Since 3 results in an answer more than 0 and 3 results in an answer less than 0, an average value is calculated for both as follows:
The f (0) is calculated and replaced with the same initial guess, depending on of the result is less than or greater than zero.
These steps are repeated successively until we reach the true value, i.e., 2 (as found using the analytical solution).
Now the question arises that if we have analytical solutions, why should we even care for finding numerical solutions? The main reason is that sometimes we dont have an analytical solution. Try to solve
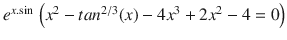
. Finding solutions would require too much human effort (may even take more than a lifetime in some cases). Moreover, complex problems involving advanced structures like differentiations, integrations, etc., are very difficult to solve using analytical solutions. For these purposes, numerical schemes have been defined.
As time progressed, various schemes to define analytical functions like differentiation, integration, trigonometric, etc., were written for digital computers. This involved their digitization, which certainly introduces some errors. Knowledge of error introduced and its proper nullification could yield valuable information quicker than using analytical results. Thus, it became one of the most actively researched fields of science and continues to be one. The search for faster and more accurate algorithms continues to drive innovation in the field of numerical computing and enables humanity to simulate otherwise impossible tasks.
1.3 Tools for Numerical Computation
While all problems can be coded in programming languages, we need to change the approach to computing, file management, etc. when we change the microprocessor platform, operating system, or both. This hinders interoperability. Modern programming languages address some of these issues but the need for specialized software for numerical computing, where predefined tools can be simply called as and when required, was being felt in academia. A number of attempts were made in this direction.
A number of alternatives exist to perform numerical computations. Programming languages written to handle mathematical functions like FORTRAN, C, Python, and Java, to name a few, can be used to write algorithms for numerical computation. Specialized software packages like MATLAB, Scilab, and Mathematica also provide specialized solutions to particular fields of problems. Their rich libraries now run in many GBs of data.
Among them, MATLAB became tremendously popular among the scientific community starting in 1984. The cheap availability of digital computing resources propelled its use in industry and academia to such an extent that virtually every lab needed MATLAB. It was embraced by academia as well as industry and in some cases, became a standard tool for computational work. An engineer who was not trained on MATLAB was less employable than others and, hence, a lot of universities adopted it in their curriculum.
But MATLAB has two serious drawbacks: its price and its licensing requirements. It started with a set of freely available tools written by academics but, when it became a commercial product, it came with a commercially restrictive license and a hefty price tag. It was the license that troubled academics more than the cost, because the license blocked sharing the software and even required an additional cost to do research work apart from teaching MATLAB.











![Ivan Idris [Ivan Idris] - NumPy Cookbook - Second Edition](/uploads/posts/book/119328/thumbs/ivan-idris-ivan-idris-numpy-cookbook-second.jpg)

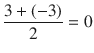
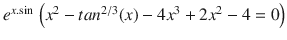 . Finding solutions would require too much human effort (may even take more than a lifetime in some cases). Moreover, complex problems involving advanced structures like differentiations, integrations, etc., are very difficult to solve using analytical solutions. For these purposes, numerical schemes have been defined.
. Finding solutions would require too much human effort (may even take more than a lifetime in some cases). Moreover, complex problems involving advanced structures like differentiations, integrations, etc., are very difficult to solve using analytical solutions. For these purposes, numerical schemes have been defined.