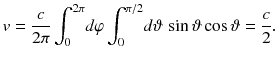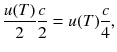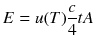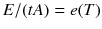1.1 Electromagnetic spectra and evidence for discrete energy levels
Quantum mechanics was initially invented because classical mechanics, thermodynamics and electrodynamics provided no means to explain the properties of atoms, electrons, and electromagnetic radiation. Furthermore, it became clear after the introduction of Schrdingers equation and the quantization of Maxwells equations that we cannot explain any physical property of matter and radiation without the use of quantum theory. We will see a lot of evidence for this in the following chapters. However, in the present chapter we will briefly and selectively review the early experimental observations and discoveries which led to the development of quantum mechanics over a period of intense research between 1900 and 1928.
The first evidence that classical physics was incomplete appeared in unexpected properties of electromagnetic spectra. Thin gases of atoms or molecules emit line spectra which contradict the fact that a classical system of electric charges can oscillate at any frequency, and therefore can emit radiation of any frequency. This was a major scientific puzzle from the 1850s until the inception of the Schrdinger equation in 1926.
Contrary to a thin gas, a hot body does emit a continuous spectrum, but even those spectra were still puzzling because the shape of heat radiation spectra could not be explained by classical thermodynamics and electrodynamics. In fact, classical physics provided no means at all to predict any sensible shape for the spectrum of a heat source! But at last, hot bodies do emit a continuous spectrum and therefore, from a classical point of view, their spectra are not quite as strange and unexpected as line spectra. It is therefore not surprising that the first real clues for a solution to the puzzles of electromagnetic spectra emerged when Max Planck figured out a way to calculate the spectra of heat sources under the simple, but classically extremely counterintuitive assumption that the energy in heat radiation of frequency f is quantized in integer multiples of a minimal energy quantum hf ,
The constant h that Planck had introduced to formulate this equation became known as Plancks constant and it could be measured from the shape of heat radiation spectra. A modern value is
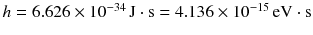
.
We will review the puzzle of heat radiation and Plancks solution in the next section, because Plancks calculation is instructive and important for the understanding of incandescent light sources and it illustrates in a simple way how quantization of energy levels yields results which are radically different from predictions of classical physics.
Albert Einstein then pointed out that equation () is accepted as an intrinsic property of electromagnetic waves, it is a small step to make the connection with line spectra of atoms and molecules and conclude that these line spectra imply existence of discrete energy levels in atoms and molecules. Somehow atoms and molecules seem to be able to emit radiation only by jumping from one discrete energy state into a lower discrete energy state. This line of reasoning, combined with classical dynamics between electrons and nuclei in atoms then naturally leads to the Bohr-Sommerfeld theory of atomic structure. This became known as old quantum theory .
Apparently, the property which underlies both the heat radiation puzzle and the puzzle of line spectra is discreteness of energy levels in atoms, molecules, and electromagnetic radiation. Therefore, one major motivation for the development of quantum mechanics was to explain discrete energy levels in atoms, molecules, and electromagnetic radiation.
It was Schrdingers merit to find an explanation for the discreteness of energy levels in atoms and molecules through his wave equation ( h 2)
A large part of this book will be dedicated to the discussion of Schrdingers equation. An intuitive motivation for this equation will be given in Section .
Ironically, the fundamental energy quantization condition ( However, we can and will discuss already now the early quantum theory of the photon and what it means for the interpretation of spectra from incandescent sources.
1.2 Blackbody radiation and Plancks law
Historically, Plancks deciphering of the spectra of incandescent heat and light sources played a key role for the development of quantum mechanics, because it included the first proposal of energy quanta, and it implied that line spectra are a manifestation of energy quantization in atoms and molecules. Plancks radiation law is also extremely important in astrophysics and in the technology of heat and light sources.
Generically, the heat radiation from an incandescent source is contaminated with radiation reflected from the source. Pure heat radiation can therefore only be observed from a non-reflecting, i.e. perfectly black body. Hence the name blackbody radiation for pure heat radiation. Physicists in the late 19th century recognized that the best experimental realization of a black body is a hole in a cavity wall. If the cavity is kept at temperature T , the hole will emit perfect heat radiation without contamination from any reflected radiation.
Suppose we have a heat radiation source (or thermal emitter) at temperature T . The power per area radiated from a thermal emitter at temperature T is denoted as its exitance (or emittance ) e ( T ). In the blackbody experiments e ( T ) A is the energy per time leaking through a hole of area A in a cavity wall.
To calculate e ( T ) as a function of the temperature T , as a first step we need to find out how it is related to the density u ( T ) of energy stored in the heat radiation. One half of the radiation will have a velocity component towards the hole, because all the radiation which moves under an angle 2 relative to the axis going through the hole will have a velocity component v ()= c cos in the direction of the hole. To find out the average speed v of the radiation in the direction of the hole, we have to average c cos over the solid angle
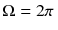
sr of the forward direction 02, 02:
The effective energy current density towards the hole is energy density moving in forward direction average speed in forward direction:
and during the time t an amount of energy
will escape through the hole. Therefore the emitted power per area
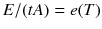
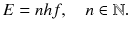
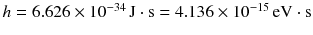 .
.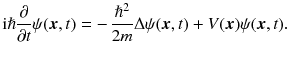
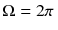 sr of the forward direction 02, 02:
sr of the forward direction 02, 02: