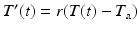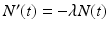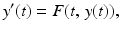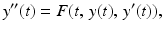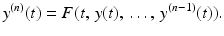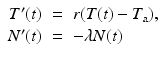Springer Science+Business Media New York 2012
William A. Adkins and Mark G. Davidson Ordinary Differential Equations Undergraduate Texts in Mathematics 10.1007/978-1-4614-3618-8_1
1. First Order Differential Equations
William A. Adkins 1 and Mark G. Davidson 1
(1)
Department of Mathematics, Louisiana State University, Baton Rouge, LA, USA
1.1 An Introduction to Differential Equations
Many problems of science and engineering require the description of some measurable quantity (position, temperature, population, concentration, electric current, etc.) as a function of time. Frequently, the scientific laws governing such quantities are best expressed as equations that involve the rate at which that quantity changes over time. Such laws give rise to differential equations. Consider the following three examples:
Example 1 (Newtons Law of Heating and Cooling).
Suppose we are interested in the temperature of an object (e.g., a cup of hot coffee) that sits in an environment (e.g., a room) or space (called, ambient space) that is maintained at a constant temperature T a. Newtons law of heating and cooling states that the rate at which the temperature T ( t )of the object changes is proportional to the temperature difference between the object and ambient space. Since rate of change of T ( t ) is expressed mathematically as the derivative, T ( t ), Newtons law of heating and cooling is formulated as the mathematical expression
where r is the constant of proportionality. Notice that this is an equation that relates the first derivative T ( t ) and the function T ( t ) itself. It is an example of a differential equation. We will study this example in detail in Sect..
Example 2 (Radioactive decay).
Radioactivity results from the instability of the nucleus of certain atoms from which various particles are emitted. The atoms then decay into other isotopes or even other atoms. The law of radioactive decay states that the rate at which the radioactive atoms disintegrate is proportional to the total number of radioactive atoms present . If N ( t ) represents the number of radioactive atoms at time t , then the rate of change of N ( t ) is expressed as the derivative N ( t ). Thus, the law of radioactive decay is expressed as the equation
As in the previous example, this is an equation that relates the first derivative N ( t ) and the function N ( t ) itself, and hence is a differential equation. We will consider it further in Sect..
As a third example, consider the following:
Example 3 (Newtons Laws of Motion).
Suppose s ( t ) is a position function of some body with mass m as measured from some fixed origin. We assume that as time passes, forces are applied to the body so that it moves along some line. Its velocity is given by the first derivative, s ( t ), and its acceleration is given by the second derivative, s ( t ). Newtons second law of motion states that the net force acting on the body is the product of its mass and acceleration . Thus,
Now in many circumstances, the net force acting on the body depends on time, the objects position, and its velocity. Thus, F { net}( t ) = F ( t , s ( t ), s ( t )), and this leads to the equation
A precise formula for F depends on the circumstances of the given problem. For example, the motion of a body in a spring-body-dashpot system is given by
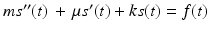
, where and k are constants related to the spring and dashpot and f ( t ) is some applied external (possibly) time-dependent force. We will study this example in Sect.. For now though, we just note that this equation relates the second derivative to the function, its derivative, and time. It too is an example of a differential equation.
Each of these examples illustrates two important points:
Scientific laws regarding physical quantities are frequently expressed and best understood in terms of how that quantity changes.
The mathematical model that expresses those changes gives rise to equations that involve derivatives of the quantity, that is, differential equations.
We now give a more formal definition of the types of equations we will be studying. An ordinary differential equation is an equation relating an unknown function y ( t ), some of the derivatives of y ( t ), and the variable t , which in many applied problems will represent time. The domain of the unknown function is some interval of the real line, which we will frequently denote by the symbol I . The order of a differential equation is the order of the highest derivative that appears in the differential equation. Thus, the order of the differential equations given in the above examples is summarized in the following table:
Differential equation | Order |
|---|
| |
| |
ms ( t ) = F ( t , s ( t ), s ( t )) | |
Note that y ( t ) is our generic name for an unknown function, but in concrete cases, the unknown function may have a different name, such as T ( t ), N ( t ), or s ( t ) in the examples above. The standard form for an ordinary differential equation is obtained by solving for the highest order derivative as a function of the unknown function y = y ( t ), its lower order derivatives, and the independent variable t . Thus, a first order ordinary differential equation is expressed in standard form as
a second order ordinary differential equation in standard form is written
and an n th order differential equation is expressed in standard form as
The standard form is simply a convenient way to be able to talk about various hypotheses to put on an equation to insure a particular conclusion, such as existence and uniqueness of solutions (discussed in Sect. ) and to classify various types of equations (as we do in this chapter, for example) so that you will know which algorithm to apply to arrive at a solution. In the examples given above, the equations













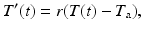
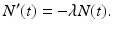
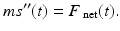
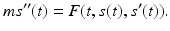
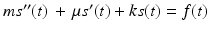 , where and k are constants related to the spring and dashpot and f ( t ) is some applied external (possibly) time-dependent force. We will study this example in Sect.. For now though, we just note that this equation relates the second derivative to the function, its derivative, and time. It too is an example of a differential equation.
, where and k are constants related to the spring and dashpot and f ( t ) is some applied external (possibly) time-dependent force. We will study this example in Sect.. For now though, we just note that this equation relates the second derivative to the function, its derivative, and time. It too is an example of a differential equation.