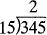Basic Business
Basic Business
Mathematics Eugene Don, M.S., Ph.D.Department of MathematicsQueens College (CUNY)Joel Lerner, M.S., Ph.D.Retired Professor of BusinessSullivan County Community College (SUNY)Schaums Outline Series New York Chicago San Francisco Lisbon
New York Chicago San Francisco Lisbon
London Madrid Mexico City Milan New Delhi
San Juan Seoul Singapore Sydney Toronto The McGraw-Hill CompaniesEUGENE DON received his B.S. from Queens College, M.S. from Columbia University, and Ph.D. in Applied Mathematics and Statistics from the State University of New York at Stony Brook. He has been a member of the Faculty of Mathematics at Queens College of the City University of New York for over 30 years, where he teaches a variety of mathematics and business mathematics courses. He has also taught courses in business at other schools in New York State.
His area of research is numerical analysis and he is interested in the application of computers to solving mathematical problems. JOEL LERNER is a retired Professor and former Chairman of the Business Division at Sullivan County Community College, Loch Sheldrake, New York. He received his B.S. from New York University and his M.S. and P.D. from Columbia University.
He has coauthored the Schaums Outlines of Principles of Accounting I and II and Business Mathematics and is the sole author of Bookkeeping and Accounting and McGraw-Hills publication of Financial Planning for the Utterly Confused, now in its fifth edition. Professor Lerner is also a financial lecturer to several Fortune 500 firms, has produced his own TV and radio series for 15 years, and addresses thousands of people annually on finances. Schaums Outline of BASIC BUSINESS MATHEMATICS Copyright 2000 by The McGraw-Hill Companies, Inc. All rights reserved. Printed in the United States of America. 6 7 8 9 0 CUS/CUS 14 3 2 ISBN 978-0-07-161158-9 MHID 0-07-161158-4 CONTENTS Preface 
Review of Arithmetic
1.1 WHOLE NUMBERS
Our number system, the decimal or base 10 system, uses the digits 0 through 9 to represent numerical values. 6 7 8 9 0 CUS/CUS 14 3 2 ISBN 978-0-07-161158-9 MHID 0-07-161158-4 CONTENTS Preface

Review of Arithmetic
1.1 WHOLE NUMBERS
Our number system, the decimal or base 10 system, uses the digits 0 through 9 to represent numerical values.
A whole number is a string of digits representing, from right to left, how many ones, tens, hundreds, thousands, ten thousands, and so on are included within the number. Commas are often used to separate groups of three digits for visual clarity. EXAMPLE 1
| The number 247 represents 2 hundreds, 4 tens, and 7 ones. |  |
EXAMPLE 2
| The number 1,547,689 represents 1 million, 5 hundred thousands, 4 ten thousands. 7 thousands, 6 hundreds, 8 tens, and 9 ones. |  |
Whole numbers are added by adding digits in corresponding columns and carrying if necessary.
The result of an addition is called the sum. Addition is most conveniently done in a vertical format and columns are added from right to left. EXAMPLE 3 To add 125, 231, and 122 we list the numbers vertically. We add the ones: 5 +1+2 = 8, the tens: 2 + 3 + 2 = 7, and the hundreds: 1 + 2 + 1 = 4. 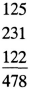 EXAMPLE 4 To add 287, 168, and 271, we add the ones: 7 + 8 + 1 = 16 (write 6 and carry 1 to the tens column), the tens: 1 + 8 + 6 + 7 = 22 (write 2 and carry 2 to the hundreds column), and the hundreds: 2 + 2 + l+ 2 = 7.
EXAMPLE 4 To add 287, 168, and 271, we add the ones: 7 + 8 + 1 = 16 (write 6 and carry 1 to the tens column), the tens: 1 + 8 + 6 + 7 = 22 (write 2 and carry 2 to the hundreds column), and the hundreds: 2 + 2 + l+ 2 = 7. 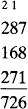 EXAMPLE 5 Find the sum of 1,367, 4,672, 1,258, and 2,116.
EXAMPLE 5 Find the sum of 1,367, 4,672, 1,258, and 2,116. 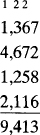 Whole numbers are subtracted by subtracting digits in corresponding columns and borrowing or exchanging if necessary.
Whole numbers are subtracted by subtracting digits in corresponding columns and borrowing or exchanging if necessary.
The result of a subtraction is called the difference. EXAMPLE 6 To subtract 237 from 579 we list the numbers vertically with the larger number on top. We subtract the ones: 9-7 = 2, then the tens: 7-3 = 4, and finally the hundreds: 5-2 = 3. In this example exchanging is not necessary. 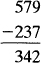 EXAMPLE 7 Subtract 257 from 492. Since 7 cannot be subtracted from 1, we exchange 1 ten for 10 ones, giving a total of 12 ones. 7 is then subtracted from 12:12 7 = 5 and the 9 in the tens column is reduced to 8.
EXAMPLE 7 Subtract 257 from 492. Since 7 cannot be subtracted from 1, we exchange 1 ten for 10 ones, giving a total of 12 ones. 7 is then subtracted from 12:12 7 = 5 and the 9 in the tens column is reduced to 8.
Then 5 is subtracted from 8: 8 5 = 3 and finally, in the hundreds column, 2 is subtracted from 4: 4 2 = 2. 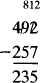 EXAMPLE 8 Find the difference between 2,257 and 1,189. Here, two exchanges are necessary. Since 9 cannot be subtracted from 7, 1 ten is exchanged for 10 ones, giving 17 in the ones column. 9 is subtracted from 17: 17 9 = 8. Since 8 cannot be subtracted from 4, one hundred is exchanged for 10 tens giving 14 in the tens column.
EXAMPLE 8 Find the difference between 2,257 and 1,189. Here, two exchanges are necessary. Since 9 cannot be subtracted from 7, 1 ten is exchanged for 10 ones, giving 17 in the ones column. 9 is subtracted from 17: 17 9 = 8. Since 8 cannot be subtracted from 4, one hundred is exchanged for 10 tens giving 14 in the tens column.
Then 8 is subtracted from 14: 14 8 = 6. 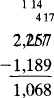 To multiply two numbers, multiply the first number (multiplicand) by each digit of the second number (multiplier). Then add. The result is called the product. The symbol for multiplication is either or . EXAMPLE 9 Multiply 54 by 23. Since the 2 in the number 23 really represents 20 its product with 54 is really 1,080.
To multiply two numbers, multiply the first number (multiplicand) by each digit of the second number (multiplier). Then add. The result is called the product. The symbol for multiplication is either or . EXAMPLE 9 Multiply 54 by 23. Since the 2 in the number 23 really represents 20 its product with 54 is really 1,080.
The rightmost 0 may be omitted and the 108 shifted one column to the left. 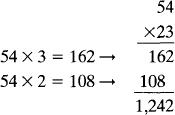 EXAMPLE 10 Multiply 112 by 245.
EXAMPLE 10 Multiply 112 by 245. 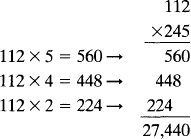 The process of division is the most complicated of the four basic arithmetic operations. We divide the dividend (the number to be divided) by the divisor (the number you are dividing by) and the result is called the quotient. The next example illustrates the process of long division. EXAMPLE 11 Divide 345 by 15. We write the problem using the standard division symbol:
The process of division is the most complicated of the four basic arithmetic operations. We divide the dividend (the number to be divided) by the divisor (the number you are dividing by) and the result is called the quotient. The next example illustrates the process of long division. EXAMPLE 11 Divide 345 by 15. We write the problem using the standard division symbol: 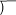 .
.
First we compare the two-digit divisor, 15, with the first two digits of the dividend, 345. Since 15 goes into 34 twice (15 2 = 30 but 15 3 is too large), we put the first digit of the quotient, 2, in the position shown. 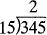
Next page




 Basic Business
Basic Business New York Chicago San Francisco Lisbon
New York Chicago San Francisco Lisbon


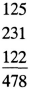 EXAMPLE 4 To add 287, 168, and 271, we add the ones: 7 + 8 + 1 = 16 (write 6 and carry 1 to the tens column), the tens: 1 + 8 + 6 + 7 = 22 (write 2 and carry 2 to the hundreds column), and the hundreds: 2 + 2 + l+ 2 = 7.
EXAMPLE 4 To add 287, 168, and 271, we add the ones: 7 + 8 + 1 = 16 (write 6 and carry 1 to the tens column), the tens: 1 + 8 + 6 + 7 = 22 (write 2 and carry 2 to the hundreds column), and the hundreds: 2 + 2 + l+ 2 = 7. 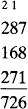 EXAMPLE 5 Find the sum of 1,367, 4,672, 1,258, and 2,116.
EXAMPLE 5 Find the sum of 1,367, 4,672, 1,258, and 2,116. 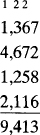 Whole numbers are subtracted by subtracting digits in corresponding columns and borrowing or exchanging if necessary.
Whole numbers are subtracted by subtracting digits in corresponding columns and borrowing or exchanging if necessary.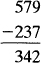 EXAMPLE 7 Subtract 257 from 492. Since 7 cannot be subtracted from 1, we exchange 1 ten for 10 ones, giving a total of 12 ones. 7 is then subtracted from 12:12 7 = 5 and the 9 in the tens column is reduced to 8.
EXAMPLE 7 Subtract 257 from 492. Since 7 cannot be subtracted from 1, we exchange 1 ten for 10 ones, giving a total of 12 ones. 7 is then subtracted from 12:12 7 = 5 and the 9 in the tens column is reduced to 8.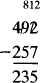 EXAMPLE 8 Find the difference between 2,257 and 1,189. Here, two exchanges are necessary. Since 9 cannot be subtracted from 7, 1 ten is exchanged for 10 ones, giving 17 in the ones column. 9 is subtracted from 17: 17 9 = 8. Since 8 cannot be subtracted from 4, one hundred is exchanged for 10 tens giving 14 in the tens column.
EXAMPLE 8 Find the difference between 2,257 and 1,189. Here, two exchanges are necessary. Since 9 cannot be subtracted from 7, 1 ten is exchanged for 10 ones, giving 17 in the ones column. 9 is subtracted from 17: 17 9 = 8. Since 8 cannot be subtracted from 4, one hundred is exchanged for 10 tens giving 14 in the tens column.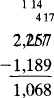 To multiply two numbers, multiply the first number (multiplicand) by each digit of the second number (multiplier). Then add. The result is called the product. The symbol for multiplication is either or . EXAMPLE 9 Multiply 54 by 23. Since the 2 in the number 23 really represents 20 its product with 54 is really 1,080.
To multiply two numbers, multiply the first number (multiplicand) by each digit of the second number (multiplier). Then add. The result is called the product. The symbol for multiplication is either or . EXAMPLE 9 Multiply 54 by 23. Since the 2 in the number 23 really represents 20 its product with 54 is really 1,080.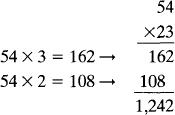 EXAMPLE 10 Multiply 112 by 245.
EXAMPLE 10 Multiply 112 by 245. 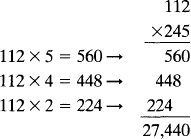 The process of division is the most complicated of the four basic arithmetic operations. We divide the dividend (the number to be divided) by the divisor (the number you are dividing by) and the result is called the quotient. The next example illustrates the process of long division. EXAMPLE 11 Divide 345 by 15. We write the problem using the standard division symbol:
The process of division is the most complicated of the four basic arithmetic operations. We divide the dividend (the number to be divided) by the divisor (the number you are dividing by) and the result is called the quotient. The next example illustrates the process of long division. EXAMPLE 11 Divide 345 by 15. We write the problem using the standard division symbol: 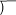 .
.