1.1 Introduction
The first branch of physical sciences that got developed by man was mechanics, i.e., the science of motion. Soon after the advent of agriculture that made assured food readily available, mankind was freed from the continuous search for food, and that provided ample free time to observe what was happening around. The simplest thing to observe is change. The change of the day to night was one such object for observation. However, the changes that man noticed around him was the change of position. Now something is here, then it is there. This subject that deals with the change of position with time is called the science of motion. This branch of physical science was the first to mature, and without exception, the students world over are exposed to the subject at an early period of their student life. The subject is of so basic a nature and so fundamental to most physical phenomena that to grasp the principles of mechanics is essential for all students of science.
However, the simplicity of the subject is elusive as the founding principles are deeply rooted in the structure of space and time. A complete understanding of that has remained unfulfilled even today. As a result, the subject, though simple from a mathematical point of view, is not easy to grasp and master. Furthermore, just feeding the students with the established formulae and training them to apply the rules mechanically at an early stage of their career leave substantial gaps in understanding. This leads to the perplexing situation when a student thinks that he/she has learnt the subject but fails miserably in examinations or is posed with a new problem.
1.1.1 Basic Parameters of Motion and Frames of Reference
Motion is the change of position with the passage of time.
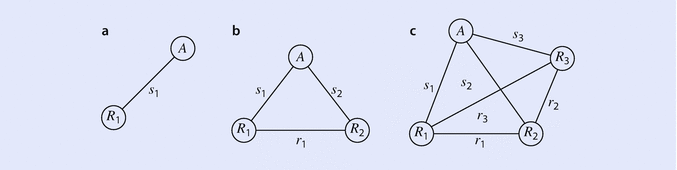
Motion is the change of position with the passage of time. Thus, motion can be perceived and studied only when position at a particular instant of time can be unambiguously identified and quantified. It is not difficult to realize that the position of an object has no meaning in empty space. It is essential to have other objects with respect to which the position of the said object has to be noted. It is again quite obvious that to avoid any ambiguity one needs more than one reference object. This is explained in Fig. b.
Fig. 1.1
Frames of reference. a Two bodies, b three bodies, c four bodies
But even in this case, A can be located anywhere on the circle that is obtained by rotating the whole structure about the line R 1 R 2. To completely specify the location of A , one needs to have another reference body R 3 located at distances r 2 and r 3 with respect to reference bodies R 2 and R 1, respectively. Now if the distance s 3 of A from R 3 is specified, the location (or position) of A with respect to the system framed by R 1, R 2, and R 3 is unambiguously determined. Such a reference system, formed by at least three reference bodies which do not possess any relative motion among themselves, is called a frame of reference. Three independent quantities are required to be specified to fix the position of a body in three-dimensional space. So a frame of reference can be defined as follows:
A frame of reference is an array of objects which do not move with respect to one another.
Thus when two players play table tennis in a moving ship, the body of the ship acts as the frame of reference. The choice of a frame of reference is based upon primarily one condition the simplicity of the description of motion. In the most suitable frame of reference, the description of a particular motion should be the simplest.
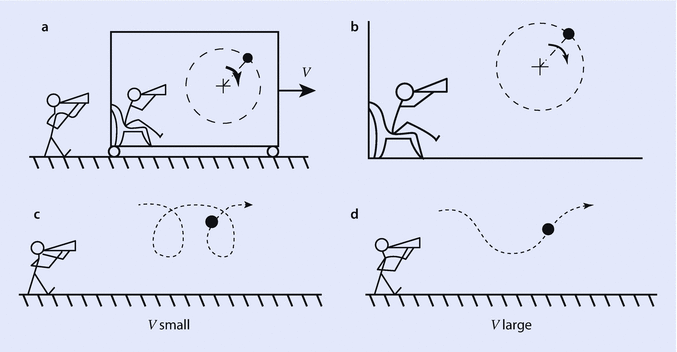
As shown in Fig. , the motion of a particle is described in two different frames of reference. When the motion is observed from the moving car, the description is simple, in the form of a circle. On the other hand, when the motion is described in a frame of reference attached to the ground, the path is more complex.
Fig. 1.2
Choice of frames of reference. a Two observers watching one phenomenon, b observation by moving observer, c observation by stationary observer for small V , d observation for large V
1.2 Mathematization of Motion
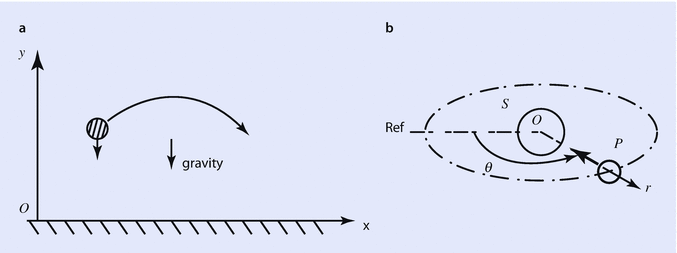
Once a motion is observed from a frame of reference, its mathematical (i.e., quantitative) description requires a coordinate system to be used. A coordinate system, again, can be different from one case to another. The coordinate system is rigidly attached to the frame of reference, and since the choice is not unique, it is based upon the simplicity of description, once again. For example, the description of motion of a projectile is convenient if a Cartesian coordinate system ( x , y ) as shown in Fig. a is used.
Fig. 1.3
Choice of coordinate system. a Rectilinear coordinate, b polar coordinate
This is so as the force acts on the particle (its weight) in a fixed direction. On the other hand, in case of the motion of a planet around the sun, a polar coordinate system ( r , ) is more convenient as the force of attraction on the planet always acts in a radially inward direction toward the sun as shown in Fig. b. Though there are quite a few different types of coordinate systems, most commonly used systems are the Cartesian ( x , y ) and the polar ( r , ) systems when the motions are confined to a plane.
1.3 Classification of Motion
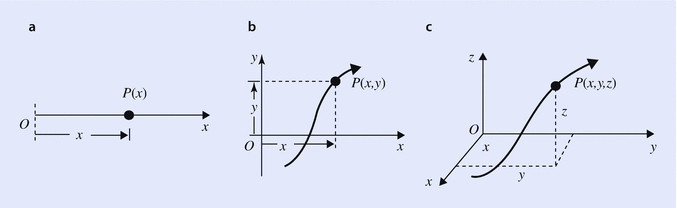
Motions can be classified according to the complexity and the basic characteristics of the path followed by a particle of the object in motion. In the simplest case, let the object under consideration be a point mass, which is called a particle. The most simple motion of a particle (from the point of view of the paths geometrical nature) is along a straight line as shown in Fig. a.
Fig. 1.4
Types of motion of a particle. a One dimensional motion, b two dimensional motion, c motion in three dimension
The description of the particle needs only one independent positional parameter x , the distance from a chosen origin O . A simple coordinate system Ox is adequate, and the motion is described by the way x changes with time. So the function x ( t ) describes the motion. In the next case, shown in Fig. b, the path of the particle can be contained in a plane in which the coordinate system Oxy is embedded. The position of the particle is defined by the way x and y vary with time, i.e., the functions x ( t ) and y ( t ). In the third and the most general case, the path requires three functions x ( t ), y ( t ), and z ( t ) for the description of motion.