Arrigo - Symmetry Analysis of Differential Equations

Copyright 2015 by John Wiley & Sons, Inc. All rights reserved

Published by John Wiley & Sons, Inc., Hoboken, New Jersey

Published simultaneously in Canada

No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permission.

Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.

For general information on our other products and services or for technical support, please contact our Customer Care Department within the United States at (800) 762-2974, outside the United States at (317) 572-3993 or fax (317) 572-4002.

Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic formats. For more information about Wiley products, visit our web site at www.wiley.com.

Library of Congress Cataloging-in-Publication Data:

Arrigo, Daniel J. (Daniel Joseph), 1960

Symmetry analysis of differential equations : an introduction / Daniel J. Arrigo, Department of Mathematics, University of Central

Arkansas, Conway, AR.

pages cm

Includes bibliographical references and index.

ISBN 978-1-118-72140-7 (cloth)

1. Lie groupsTextbooks. 2. Lie groupsStudy and teaching (Higher) 3. Lie groupsStudy and teaching (Graduate) 4. Differential

equations, PartialTextbooks. I. Title.

QA387.A77 2014

515.353dc23

2014007305

Printed in the United States of America.

10 9 8 7 6 5 4

To the late Bill Ames,

my teacher, my mentor, my friend.

Have you ever wondered whether there is some underlying theory that unifies all the seemingly ad-hoc techniques that are used to solve first-order ordinary differential equations (ODEs)? In the 1880s Sophus Lie did [51]. He was able to show that a majority of the techniques used to integrate ODEs could be explained by a theory known as Lie group analysis, where the symmetries of a differential equation could be found and exploited.

This is a self-contained introductory textbook on Lie group analysis, intended for advanced undergraduates and beginning graduate students, or anyone in the science and engineering fields wishing to learn about the use of symmetry methods in solving differential equations. This book has many detailed examples, from the very basic to the more advanced, guiding one through the method of symmetry analysis used for differential equations. The methods presented in this book are very algorithmic in nature, and the author encourages the reader to become familiar with one of the computer algebra packages, such as Maple or Mathematica to help with the calculations, as they can get extremely long and tedious.

The material presented in this book is based on lectures given by the author over the last 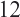years at the University of Central Arkansas (UCA). This book consists of four chapters. In Chapter 1, the reader is introduced to the idea of a symmetry and how these symmetries can leave objects invariant and, in particular, differential equations.

Chapter 2 concentrates on constructing and exploiting symmetries of ordinary differential equations. In particular, the focus is on standard techniques for integrating first-order ODEs: linear, Bernoulli, homogeneous, exact, and Riccati equations are considered. This chapter then considers symmetry methods for second-order equations, higher order equations, and systems of ordinary differential equations.

Chapter 3 extends the ideas to partial differential equations (PDEs). This chapter starts with first-order PDEs and then graduates to second-order PDEs. The power of the method is seen in this chapter, where the heat equation with a source term is considered. This chapter then moves to higher order PDEs and systems of PDEs, where several of the examples (and exercises) have been chosen from various fields of science and engineering.

The last chapter, Chapter 4, starts with a discussion of the nonclassical methoda generalization of Lie's classical method and then shows its connection with compatibility. Finally, this chapter ends with a very brief discussion what's beyond.

Each chapter has a number of exercises; some are routine while others are more difficult. The latter are denoted by . Many of the answers are given, and for some of the harder or more elaborate problems, a reference to theliterature is given.

The material presented in Chapters 13 is more than enough for a one-semester course and has been the basis of the course given here at UCA over the last 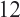years.

Lastly, for further information and details, including available programs, it is encouraged that you please visit the book's accompanying website at symmetrydes.com.

1. 1. Lie S, Klassifikation und Integration von gewohnlichen Differentialgleichen zwischen 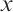, 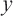die eine Gruppe von Transformationen gestatten, Math. Ann. 213281 (1888).

First and foremost, I wish to extend my thanks to W.F. Ames. He was the first to expose me to the wonderful world of the symmetry analysis of differential equations during my PhD studies at Georgia Tech. His patience and support was never ending. I was fortunate to work with Phil Broadbridge and Jim Hill at the University of Wollongong (Australia) for several years while I was a post-doc. I learned so much from them. As this book emerged from lecture notes for a course that I've taught at the University of Central Arkansas, I wish to thank all my students over the past dozen years for their valuable input. In particular, I thank Regan Beckham, David Ekrut, Jackson Fliss, Luis Suazo, and Bode Sule, who were all student researchers and became my coauthors. I would also like to thank David Ekrut and Crystal Spellmann, who read a large portion of this manuscript and gave me valuable suggestions. I would also like to thank Susanne Steitz-Filler with John Wiley & Sons. She helped make this work come to life and helped make the transition so easy.