This book studies geometry methodically from an analytical , i.e., coordinate-based, viewpoint. In many settings this approach simplifies the computer representation of geometric data. We shall not confine ourselves to linear problems. This is not only appealing from a theoretical viewpoint, it is also practically motivated by advances in computer algebra and the availability of fast computer hardware.
In Chapter we will lay some mathematical foundations. First, we will introduce the language of projective geometry , which is very well suited for many geometric applications. Since this is not usually covered in standard introductory courses in mathematics, we briefly discuss the central concepts of projective spaces and projective transformations. We will also introduce the notion of convexity in this chapter.
Our analytical approach motivates the structure of this book. It is centered around questions about algorithms which solve systems of equations and their increasingly complex variations with regard to the required mathematical tools.
1.1 Linear Computational Geometry
Most algorithms described in this book are based on Gaussian elimination , a core topic in any linear algebra course. In geometric language Gaussian elimination is a procedure which takes a set of affine hyperplanes, H 1,, H k , in the vector space K n as input, where K is an arbitrary field. If
the output can be an (affine) basis for A , or simply its dimension.
Our foray through computational geometry begins with the real numbers and the transition from equalities to inequalities. Consider for every hyperplane
the closed half-space
The intersection
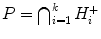
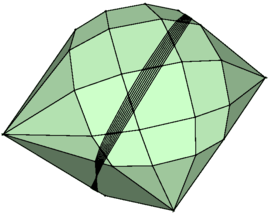
defines a ( convex ) polyhedron (see Fig. for an example in 3).
Fig. 1.1
An example of a bounded polyhedron in 3. This particular polyhedron is a polytope which is dual to a zonotope. The belt-like strip in the middle has several very thin facets
Polyhedra are fundamental to computational geometry and linear optimization. In higher dimensions, the combinatorial variety of polyhedra is considerably larger than that suggested by lower dimensional images, such as Fig.. One of the fundamental questions when determining the complexity of many algorithms is, what is the maximum number of vertices that a polyhedron defined by k linear inequalities can have? This question was first answered in 1970 by the Upper-bound Theorem . The proof (in a somewhat weaker formulation, see Theorem 3.46) and the explanation of the underlying geometric structure is the first goal of this book. This result is particularly important for computational geometry because we can use it to obtain complexity estimates for several algorithms.
In Chapter we systematically study the properties of polytopes (face lattice, polarity, combinatorics of polytopes) up to Eulers formula and the DehnSommerville equations . At the end of the chapter we illustrate some of the concepts with the geometric software polymake . We will also use this and other software as an aid to understanding the algorithms presented in later chapters.
The core of many mathematical applications is linear optimization, which addresses the problem of computing the minimum or maximum of a linear objective function on a polyhedron P (given by linear inequalities). For computational solutions it is important to note that the polyhedron can be empty, or the objective function can be unbounded on P . In Chapter we give a brief introduction to the relevant aspects of linear optimization. In particular, we discuss the theoretically and practically important simplex algorithm . Our main focus (as throughout this text) will be from the geometric perspective.
An interesting computational problem of polytope theory is determining the entire set of vertices and rays of a polyhedron defined by a given set of inequalities. Using the duality theory described in Section to the convex hull problem . For applications it is important to note that actually computing solutions to this problem becomes difficult in higher dimensions (simply because of the large output predicted by the Upper-bound Theorem). A general approach for efficient algorithms is the divide-and-conquer principle. We illustrate this by applying it to the computation of convex hulls in the plane.
Next, we examine Voronoi diagrams and the corresponding dual Delone subdivisions . Given an arbitrary point set S ={ s (1),, s ( m )} in the n -dimensional space n , the Voronoi region corresponding to a point s ( i ) comprises those points of n which are no further from s ( i ) (with respect to Euclidean distance) than from any other point of S .
In Chapter we first show how convex hull algorithms can be used to compute Voronoi diagrams in arbitrary dimensions. Afterwards, we concentrate again on the planar case and present the beach line algorithm . Knowledge of abstract data types is an advantage for this, so the most important principles will be explained. For a more in depth discussion of common data structures the reader can refer to the recommended literature.
Voronoi diagrams can be used to solve the so-called post office problem ; a classical application of computational geometry. Given a finite set of points S 2, we efficiently compute for each point p 2 the point s S which minimizes the Euclidean distance p s . The points of S can be interpreted as post offices and the points p as customers. See Fig.. Of course, one can naively examine every point combination (which is efficient if there is only one customer). However, one should interpret the problem as if the postal service wants to create an information system which quickly provides answers for a large group of customers, assuming that the positions of the post offices do not change.

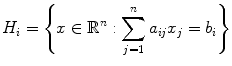
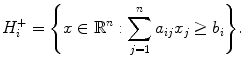
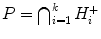 defines a ( convex ) polyhedron (see Fig. for an example in 3).
defines a ( convex ) polyhedron (see Fig. for an example in 3).