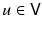1. Introduction
The solution of large systems of linear equations,
is a ubiquitous task in scientific computing, forming the core computational kernel of scientific computations arising from a broad range of applications. One remarkable application, and the one for which multigrid (MG) was originally devised, is the numerical solution of some partial differential equation (PDE),
specified with suitable boundary conditions on some domain
. After discretizing the infinite-dimensional problem () to be solved (at each time step, if time is involved).
Algebraic multigrid (AMG) is a class of iterative methods for solving such linear systems, specifically those that are sparse, as is the case, for example, for typical discretizations of PDEs by grid-based methods. When applicable, AMG is often able to produce a numerical solution using a number of operations scaling linearly or nearly linearly in the number of unknowns. Our specific interest is in AMG applied to inherently nonsymmetric problems, for example, discretized convection-diffusion equations with high Pclet number (convection-dominated), as opposed to, say, a nonsymmetric discretization of Poissons equation. Most of the AMG analysis that has been done, with Notays work being a notable exception, has been for the symmetric case. Analysis is essential for the development of improved, more robust, and more broadly applicable AMG methods.
We present in Chap..
In this chapter we first look at the simplest of symmetric model problems, Poissons equation, and briefly cover its discretization by the finite element method (FEM) and its solution by geometric multigrid. The purpose is to introduce in the simplest concrete setting all of the concepts that we will make use of later, including the variational setting, linear iterative methods, and multigrid in its general conception. We then look at a nonsymmetric model problem, advection-diffusion, as well as its discretization, which we will use to illustrate and test the abstract theory of later chapters. All of this material is background. Also, for the most part, later chapters can be read independently of the material here.
1.1 A Symmetric Model Problem
This section focuses on Poissons equation. We begin with a brief presentation of the finite element method (FEM) for this equation, before presenting geometric multigrid applied to the resulting problem. We end with the main ideas of the multigrid convergence theory due to Hackbusch. This is background material, dealing only with a specific, symmetric model problem, and only with geometric multigrid. The intent is to introduce and motivate, in a concrete setting, the ideas we will need in later chapters.
Algebraic multigrid (AMG) methods make as few assumptions about the input matrix as possible, and are certainly not limited to matrices resulting from finite element discretizations. However, one of the key elements of AMG, the Galerkin (or Petrov-Galerkin) coarse operator construction, is directly analogous to the finite element discretization procedure, which comes about from the variational setting in which the FEM is based. The analysis of later chapters will be rooted in just such a variational setting. The presentation of FEM here is meant to provide a concrete introduction to these concepts, not to rule out applicability of the material of later chapters to other discretizations.
1.1.1 Abstract Formulation of Poissons Equation
Let us consider the problem of finding a solution to Poissons equation on a bounded open subset
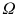
of

with Lipschitz continuous boundary
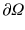
:
A modern approach is to look for solutions u in a suitable function space. As usual, we will use the Sobolev space
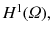
the subset of
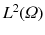
consisting of those functions with weak first derivatives also in
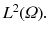
The Dirichlet boundary conditions narrow the solution space to
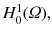
the subspace of
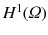
of functions whose trace on
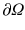
vanishes. The variational form of () reads: given
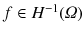
, find
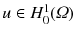
such that
where
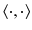
denotes the
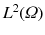
inner product.
In this and following chapters, the concept of dual space will play a fundamental role. Recall that the continuous dual of a Banach space
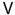
, denoted by
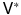
, consists of all continuous linear functionals on
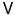
. Each element
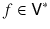
maps each vector
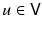













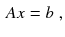
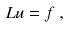
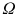 . After discretizing the infinite-dimensional problem () to be solved (at each time step, if time is involved).
. After discretizing the infinite-dimensional problem () to be solved (at each time step, if time is involved).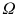 of
of  with Lipschitz continuous boundary
with Lipschitz continuous boundary 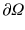 :
: 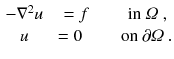
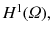 the subset of
the subset of 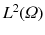 consisting of those functions with weak first derivatives also in
consisting of those functions with weak first derivatives also in 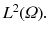 The Dirichlet boundary conditions narrow the solution space to
The Dirichlet boundary conditions narrow the solution space to 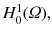 the subspace of
the subspace of 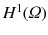 of functions whose trace on
of functions whose trace on 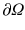 vanishes. The variational form of () reads: given
vanishes. The variational form of () reads: given 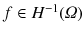 , find
, find 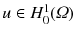 such that
such that 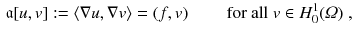
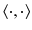 denotes the
denotes the 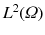 inner product.
inner product.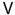 , denoted by
, denoted by 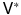 , consists of all continuous linear functionals on
, consists of all continuous linear functionals on 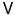 . Each element
. Each element 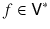 maps each vector
maps each vector