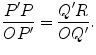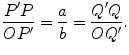1. The Birth of Analytic Geometry
Today it is often thought that the original idea of plane analytic geometry was to identify a point of the plane via two coordinates. This is certainly part of the truth, but just a very small part. The problem at the origin of analytic geometry was much deeper: every equation in two variables represents a curve in the plane, and conversely .
Plane analytic geometry was introduced independently by the French mathematicians Fermat and Descartes around 1630. The solution of a geometric problem by the methods inherited from the Greek geometersthat is, via constructions with ruler and compassoften required incredible imagination and could by no means be systematised. Fermat and Descartes showed that many of these geometric problems could be solved instead by routine algebraic computations. However, in those days, efficient algebraic techniques were still to be invented and good systems of coordinates were still to be discovered. The absence of these essential ingredients led rapidly to rather indigestible computations and proofs, in particular when mathematicians tried to switch to the three dimensional case.
For example, the equation of a conic becomes rather easy when you choose a system of coordinates inspired by the various symmetries of the curve. This is the so-called problem of the reduction of the equation of a conic . But mathematicians of the 17th century could hardly do that, since for them a coordinate had to be a positive number: thus it was impossiblefor exampleto choose the center of a circle as origin to express the equation of the full circle! Moreover, handling changes of coordinates centuries before the discovery of matrices and determinants was certainly not an easy job!
From the very beginning of analytic geometry, special attention was also paid to the equation of the tangent to a curve given by a polynomial equation. The problem of the tangent was generalized a century later to the case of arbitrary curves, via the development of differential calculus; we shall study this problem in Sect. 2.4 of [], Trilogy III . Nevertheless, it is interesting to observe how some basic ideas of modern algebraic geometry or differential geometry were already present, from the very beginning, in the work of Fermat and Descartes.
Another ideaessentially due to Euler, during the 18th centurywas to express the various coordinates of the points of a curve in terms of a single parameter: these so-called parametric equations again constitute a basic ingredient of modern differential geometry.
Let us also mention that various other non-Cartesian systems of coordinates were considered during the 18th century: polar, bipolar, cylindrical, spherical, and so on. These systems do not have the universal character of Cartesian coordinates and their possible efficiency, in some specific problems, is strongly limited to those cases presenting evident symmetries with respect to the chosen system.
The introduction of coordinates in the plane, by Fermat and Descartes, of course made use of an axis (or at least, directions in the plane) forming a certain non-zero angle; the coordinates were obtained by measuring distances in the directions of these axis. Thus it was accepted at once that the plane was equipped with two notions of distance and angle and these were used intensively. Recognizing that these two notions can themselves appear as by-products of some bilinear form defined on
a so-called scalar product has further opened the way to the use of deep algebraic theorems to handle geometric problems.
Of course, for this approach in terms of bilinear forms to be given full strength and generality, it was another important step to relate geometric space with the abstract notion of vector space and, eventually, of affine space over an arbitrary field. Recognizing the possibility of developing geometry over an arbitrary base field provided in particular a unified treatment of both real and complex geometry.
We conclude this chapter with a detailed account of conics and quadrics : respectively, the curves of degree 2 in the real plane and the surfaces of degree 2 in real three dimensional space.
1.1 Fermats Analytic Geometry
The French mathematician Pierre de Fermat (16011655) had probably developed his analytic geometry not later than 1629 and his results circulated in manuscript form for some fifty years. It was only several years after his death, in 1679, that the manuscript was eventually published.
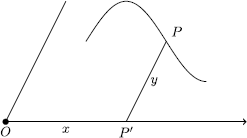
Fermat considers a half-line with origin O and a direction other than that of the line (see Fig. ). Given a point P of a curve, he draws PP parallel to the chosen direction and locates the point P via the two distances x = OP and y = P P . Let us stress the fact that Fermat considers only positive values for the distances x and y . This apparently minor limitation will prove to be a serious handicap to an efficient development of analytic geometry.
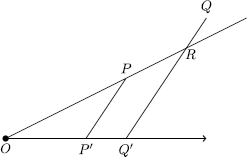
Fermats first preoccupation is to prove that an equation of the form ax = by represents a straight line through the origin O . Indeed if P and Q are two points of the curve ax = by , let P , Q be their corresponding projections on the base half-line (see Fig. ). Calling R the intersection of the lines OP and Q Q , the similarity of the triangles OP P and OQ R yields
On the other hand, since P and Q are on the curve ax = by , we obtain
It follows at once that Q R = Q Q and thus R = Q . This proves that O , P , Q are on the same line.
Next Fermat considers the case of the equation ax + by = c 2 which he provesby analogous argumentsto be the equation of a segment. Indeed, let us recall that for Fermat, the letters a , b , c , x , y represent positive quantities: this is why the values of x and y are bounded and the corresponding curve is only a segment, not the whole line. Nevertheless, the use of c 2 in the equation, instead of just c , is worth a comment. Fermat wants to introduce algebraic methods, but he is still very strongly under the influence of Greek geometry. The quantities a , b , x , y represent distances, thus the product quantities ax , by represent areas; and an area ax + by cannot be equal to a length c : it has to be compared with another area c 2!
After considering equations of the first degree, Fermat switches to the second degree and intends to show that the equations of the second degree represent precisely the (possibly degenerate) conics. Indeed Fermat knows, by the work of the Greek geometers Menechmus and Apollonius , that every conic admits an equation of degree 2; to prove the converse, Fermat first considers some special cases.
