Pinaki Mondal - How Many Zeroes?: Counting Solutions of Systems of Polynomials via Toric Geometry at Infinity

CMS/CAIMS Books in Mathematics is a collection of monographs and graduate-level textbooks published in cooperation jointly with the Canadian Mathematical Society- Societ mathmatique du Canada and the Canadian Applied and Industrial Mathematics Society-Societ Canadienne de Mathmatiques Appliques et Industrielles. This series offers authors the joint advantage of publishing with two major mathematical societies and with a leading academic publishing company. The series is edited by Karl Dilcher, Frithjof Lutscher, Nilima Nigam, and Keith Taylor. The series publishes high-impact works across the breadth of mathematics and its applications. Books in this series will appeal to all mathematicians, students and established researchers. The series replaces the CMS Books in Mathematics series that successfully published over 45 volumes in 20 years.

More information about this series at http://www.springer.com/series/16627

This Springer imprint is published by the registered company Springer Nature Switzerland AG

The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland

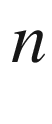In this book we describe an approach through toric geometry to the following problem: estimate the number (counted with appropriate multiplicity) of isolated solutions of polynomial equations in 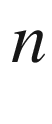variables over an algebraically closed field . The outcome of this approach is the number of solutions for generic systems in terms of their Newton polytopes, and an explicit characterization of what makes a system generic. The pioneering work in this field was done in the 1970s by Kushnirenko, Bernstein and Khovanskii, who completely solved the problem of counting solutions of generic systems on the torus 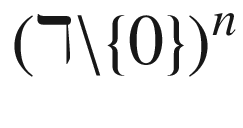. In the context of our problem, however, the natural domain of solutions is not the torus, but the affine space 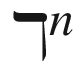. There were a number of works on extending Bernsteins theorem to the case of affine space, and recently it has been completely resolved, the final steps having been carried out by the author.

The aim of this book is to present these results in a coherent way. We start from the beginning, namely, Bernsteins beautiful theorem which expresses the number of solutions of generic systems on the torus in terms of the mixed volume of their Newton polytopes. We give complete proofs, over arbitrary algebraically closed fields, of Bernsteins theorem, its recent extension to the affine space, and some other related applications including generalizations of Kushnienkos results on Milnor numbers of hypersurface singularities which in 1970s served as a precursor to the development of toric geometry. Our proofs of all these results share several key ideas and are accessible to someone equipped with the knowledge of basic algebraic geometry. This book can serve as a companion to introductory courses on algebraic geometry or toric varieties. While it does not provide a comprehensive introduction to algebraic geometry, it does develop the relevant parts of the subject from the beginning (modulo some explicitly stated basic results) with lots of examples and exercises and can be used as a quick introduction to basic algebraic geometry. We hope the readers who take that undertaking will be rewarded by a deep understanding of the affine Bzout problem.