1.1 Sets
To study analysis successfully, the reader must be conversant with some of the basic concepts of mathematics. Foremost among these is the idea of a set. For our purposes a set may be thought of as a collection of objects. This statement is too imprecise to be regarded as a definition, and in fact it leads to logical difficulties, but it does convey a mental image of a set that is satisfactory for our purposes. The reader who wishes to delve into the nature of this concept more deeply is referred to [].
Sets are important in that they can be used to construct a host of mathematical concepts. In fact, every mathematical object studied in this book can be constructed from sets. We therefore begin this introductory chapter with some basic properties of sets. Proofs are omitted because most of the properties are evident and their proofs are straightforward.
First, the objects in a set X are called its elements or members . They are said to be contained in X and to belong to X . If an object x is contained in X , then we write x X ; otherwise we write x X .
We shall assume the existence of a set with no elements. This set is denoted by , and it is unique. It is said to be empty .
If X and Y are sets such that every element of X is also an element of Y , then we say that X is a subset of Y and that it is included in Y . In this case we write X Y ; otherwise we write X Y . Note that X for every set X . The reasoning is that since has no elements at all, it certainly has no elements that are not in X . Therefore we can safely say, without fear of contradiction, that each of its elements does belong to X . In particular, is a subset of itself, and in fact it is its only subset. Observe also that every set includes itself. Moreover, if X , Y , Z are sets such that X Y and Y Z , then X Z . In this case we write X Y Z .
If X and Y are sets such that X Y X , then X and Y contain exactly the same elements. In this case we say that these sets are equal , and we write X = Y . Otherwise X and Y are distinct , and we write X Y . Any set is equal to itself, and if X = Y , then Y = X . Furthermore, if X , Y , Z are sets such that X = Y and Y = Z , then X = Z . In this case we write
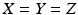
. Equal sets are treated as identical since they contain the same elements.
The collection of all subsets of a given set X is another set, called the power set of X . It is denoted by
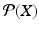
. For example,
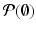
is a set having as its only element. This set is denoted by {}. Moreover,
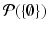
is a set containing only the elements and {} and is denoted by {,{}}.
If X is any set, we may replace the elements of X by other objects and thereby construct a new set. For example, we may replace the unique element of the set {} by any object Y . We then have a new set whose only element is Y . This set is denoted by { Y }. Similarly, if we replace the elements and {} of the set {,{}} by objects Y and Z , respectively, then we obtain a new set whose only elements are Y and Z . This set is denoted by { Y , Z }. The notation may be extended to an arbitrary number of objects.
If X is a set and P is a property that may be satisfied by some elements of X , then we can construct a subset of X whose elements are precisely the members of X that do satisfy P . This set is denoted by { x X P }. For example, let X and Y be sets, and let P be the property that x Y , where x X . Then { x X P } is the set whose elements are the objects that are in both X and Y . This set is called the intersection of X and Y and is denoted by X Y . If this intersection happens to be empty, then the sets X and Y are disjoint . If
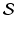
is a collection of sets (in other words, a set whose elements are themselves sets), then the sets in
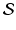
are said to be mutually disjoint if the sets A and B are disjoint whenever
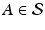
and
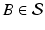
.
On the other hand, if P is the property that x Y , then { x X P } is the set whose elements are the members of X that are not in Y . This set is denoted by X Y and is called the complement of Y with respect to X .
Let
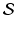
be a collection of sets. Then we may construct another set whose elements are the objects that belong to at least one member of
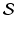
. This set is called the union of
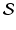
. For example, if
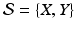
for some sets X and Y , then the union of
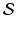
is the set of all objects that are in X or Y . In particular, it contains all the objects that are in both of those sets. It is denoted by X Y .
We may define the intersection of
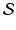
as the set of all objects in the union of
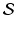
that belong to every set in
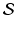
. If
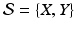
for some sets X and Y , then the intersection of
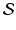
is the set of all objects that are in both X and Y . Thus it is equal to X Y .
1.2 Ordered Pairs, Relations, and Functions
As we said before, sets can be used to construct a large number of mathematical concepts. In this section we show how to construct ordered pairs, relations, and functions from sets, but once again the reader is referred to [] for the details.
If x and y are any objects, then the ordered pair ( x , y ) is defined as the set {{ x },{ x , y }}. We refer to x and y as its components , x being the first component and y the second . The important observation to be made here is that the definition does not treat x and y similarly (if in fact they are distinct objects). Instead, we are given a way of distinguishing them: y is a member of just one of the two sets in ( x , y ), but x belongs to both sets. From this observation it is easy to deduce that the ordered pairs ( x , y ) and ( a , b ) are equal if and only if x = a and y = b . In other words, for equality to hold it is not sufficient for the sets { x , y } and { a , b } to be equal. Their elements must also be listed in the same order. This is the only property of ordered pairs that is important to remember. Once it is grasped, the definition may be forgotten. The definition can be extended to ordered triples by defining














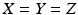 . Equal sets are treated as identical since they contain the same elements.
. Equal sets are treated as identical since they contain the same elements.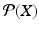 . For example,
. For example, 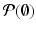 is a set having as its only element. This set is denoted by {}. Moreover,
is a set having as its only element. This set is denoted by {}. Moreover, 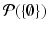 is a set containing only the elements and {} and is denoted by {,{}}.
is a set containing only the elements and {} and is denoted by {,{}}.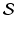 is a collection of sets (in other words, a set whose elements are themselves sets), then the sets in
is a collection of sets (in other words, a set whose elements are themselves sets), then the sets in 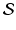 are said to be mutually disjoint if the sets A and B are disjoint whenever
are said to be mutually disjoint if the sets A and B are disjoint whenever 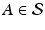 and
and 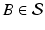 .
.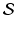 be a collection of sets. Then we may construct another set whose elements are the objects that belong to at least one member of
be a collection of sets. Then we may construct another set whose elements are the objects that belong to at least one member of 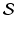 . This set is called the union of
. This set is called the union of 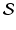 . For example, if
. For example, if 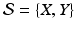 for some sets X and Y , then the union of
for some sets X and Y , then the union of 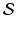 is the set of all objects that are in X or Y . In particular, it contains all the objects that are in both of those sets. It is denoted by X Y .
is the set of all objects that are in X or Y . In particular, it contains all the objects that are in both of those sets. It is denoted by X Y .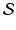 as the set of all objects in the union of
as the set of all objects in the union of 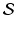 that belong to every set in
that belong to every set in 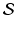 . If
. If 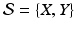 for some sets X and Y , then the intersection of
for some sets X and Y , then the intersection of 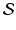 is the set of all objects that are in both X and Y . Thus it is equal to X Y .
is the set of all objects that are in both X and Y . Thus it is equal to X Y .