2D Game Collision Detection
An introduction to clashing geometry in games
Thomas Schwarzl
Table of Contents
Introduction
Are you curious how 2D collision detection ingames works? If so this book is made for you.
In case you don't know what collision detectionis: it's the determination of whether objects simulated in programscollide. This is a basic feature of computer games, e.g. fordetermining shot impacts, finding out which enemies are covered bylines of sight, recognizing collisions of race cars or simplychecking if the mouse cursor floats above a button.
The book is written for game developers but issuited for other coder species as well.
Featuresof This Book
This book was written with the followingintentions in mind:
- be aimed at beginners,
- use successive knowledge building,
- leverage a picture paints a thousand words,
- provide working code,
- allow it to also function as a reference book and
- enable fast navigation by cross-linking
This book has less than 100 pages. That's not muchfor a textbook. Nonetheless, that's intentional. Serving up thenecessary information on a minimum of pages is better than throwing a500+ page tome at you. Brevity is the soul of wit.
YouWill Need
... knowledge in basic procedural programming. Allcode is written in the language C. C is the "mother" ofmodern imperative programming languages. So the language choice forthis book was a no-brainer. If you're more familiar with C++, Java,Objective-C or C# you won't have any problems understanding what'sgoing on in this book.
The code was written for comprehensibility. Somedetails were simplified or left out to get short and understandablecode. Therefore the book's code may not be 100% correct C code.
Further there are no optimizations or fancy tricksin the code. That would compromise understandability.
Check out the ,which provides all code from this book as a download.
YouWon't Need
... an academic degree. As long as you understandaddition, multiplication and can read equations you should notencounter any problems throughout this book.
Oh, wait! You'll need to know what a square rootis.
And what's PI.
I'm afraid elementary school children are out.Sorry.
ShareYour Thoughts
If you have any questions about the book,collision detection or programming in general just drop me a line.Critique, praise and professional curses are welcome as well:
I'm looking forward to hearing from you.
Atomsof Geometry: Vectors
Game objects need physical representations. Gamesuse diverse geometric shapes for this. To find out if two objectscollide we just have to check if their shapes intersect.
In computer games shapes usually get described byvectors. They are the building blocks for shapes and collisiondetection. So we first have to understand vectors and what we can dowith them before we can tackle shapes and collision detection.
What Vectors Are
In 2D space a vector is simply a displacement intwo dimensions. Vectors have length and direction but no position. Asimple definition for 2-dimensional vectors is:
A 2D vector describes a straight movement in 2D space.
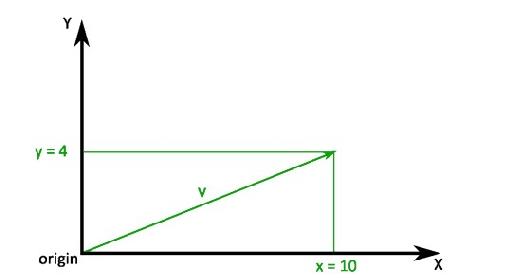
The two dimensions are called X and Y. Thefollowing illustration and code shows exemplary 2D vector v:
typedef struct
{
float x;
float y;
} Vector2D;
Vector2D v = {10, 4};
The black arrows represent the coordinate systemaka 2D space. The horizontal arrow illustrates the X-axis of thecoordinate system, the vertical one illustrates axis Y. Their sharedstarting point is called the origin. The position of theorigin is always {0, 0}.
We will use notation {x, y} for vectors throughout the whole book. It's the same notation used for initializing vectors in code. Examples for this notation are {10, 4}, {-208, 13} or {0, -47.13}.
Vector v goes from the origin 10units along axis X and 4 units along axis Y. Using our vectornotation:
v = {10, 4}
This is the very same expression you can find inthe code example above.
The vectors origin and v can also be seen as points in the coordinate system. The words pointand vector are interchangeable in this case.
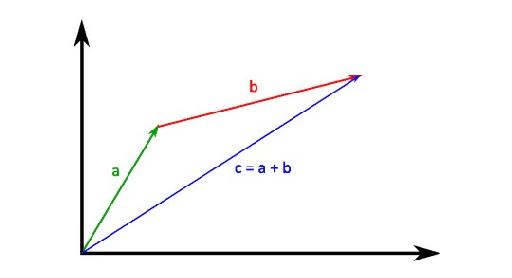
Additions
Vector addition can be imagined as chainingvectors. As mentioned in , a vector is a displacement in 2D space. Let'sassume we have point a, add vector b and get theresulting point c:
Vector2D add_vector(Vector2D a, Vector2D b)
{
Vector2D r;
r.x = a.x + b.x;
r.y = a.y + b.y;
return r;
}
Vector2D a = {3, 5};
Vector2D b = {8, 2};
Vector2D c = add_vector(a, b);
Vector c points to the position whichvector a points to after it is displaced by vector b.This displacement is known as vector addition or, in math tongue,vector translation.
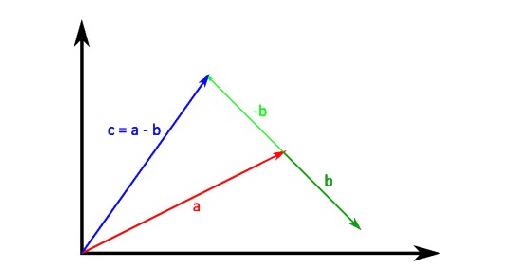
Now that we know how vector addition works, whatabout vector subtraction?
Subtraction is as simple as addition:
Vector2D subtract_vector(Vector2Da, Vector2D b)
{
Vector2D r;
r.x = a.x b.x;
r.y = a.y b.y;
return r;
}
Vector2D a ={7, 4};
Vector2D b = {3, -3};
Vector2D c =subtract_vector(a, b);
Subtraction can also be seen as adding a negatedvector. In our case it would be adding negative b to a:
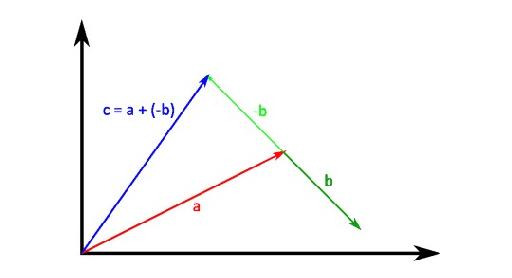
typedef enum { no = 0, yes = 1 }Bool;
Vector2D negate_vector(Vector2D v)
{
Vector2D n;
n.x = -v.x;
n.y = -v.y;
return n;
}
Bool equal_floats(float a, float b)
{
float threshold = 1.0f / 8192.0f;
return fabsf(a - b) < threshold;
}
voidassert_equal_vectors(Vector2D a, Vector2D b)
{
assert(equal_floats(a.x, b.x));
assert(equal_floats(a.y, b.y));
}
Vector2D a = {7, 4};
Vector2D b = {3, -3};
Vector2D c = add_vector(a,negate_vector(b));
assert_equal_vectors(c, subtract_vector(a,b));
This code needs a little bit of explanation. Firstdata type Bool is defined. It has just two possible values:yes and no. Any logical statement will return one ofthese two values.
If you're familiar with C youmay ask: "Why not use well known true and false?".The terms yes and no were adopted from Objective-Cbecause they are more readable.
Function negate_vector() should beself-explanatory: it takes a vector and returns it pointing in theopposite direction.
Function equal_floats() andassert_equal_vectors() are test functions. The former returnsyes when the two parameters are equal. The latter checks iftwo vectors are equal. If not, function assert() is used tosignal an error.
Functions equal_floats(),assert_equal_vectors() and assert() will often be usedthroughout the book. The basic function assert() - whichexperienced coders surely know takes the result of anassertion as a parameter. If the assertion is true the function doesnothing. If it's wrong the function signals a problem, e.g. showing asmall message box stating an error message. Function






![Gabor Szauer [Gabor Szauer] - Game Physics Cookbook](/uploads/posts/book/121399/thumbs/gabor-szauer-gabor-szauer-game-physics-cookbook.jpg)
![Rex van der Spuy [Rex van der Spuy] - Foundation Game Design with HTML5 and JavaScript](/uploads/posts/book/121398/thumbs/rex-van-der-spuy-rex-van-der-spuy-foundation.jpg)
![Dave Mathews [Dave Mathews] - Panda3D 1.6 Game Engine](/uploads/posts/book/118496/thumbs/dave-mathews-dave-mathews-panda3d-1-6-game.jpg)








