1. Introduction
An attempt to look at quantum theory from a different perspective also leads to the question of where the idea of quantization, i.e., dividing our material world into smallest building blocks, actually originates. In the western hemisphere this takes one back to ancient Greece and its philosophers. In this case, one might first think of Democritus (ca. 460ca. 371 B.C.) who coint the term atomos for the smallest building blocks of matter which cannot be divided any further. The word atom remains today. However, the atom turned out to be composed of even smaller constituents and, at present we are at the level of quarks and gluons. Is this the end, or will it be possible to detect yet smaller components with higher energized accelerators? Maybe we are even searching for the wrong answer and should not be looking for the smallest material particle but rather for some general elementary structure(s) that are ubiquitous in the universe and not depending on the size!
Another Greek philisopher even more famous than Democritus was probably thinking more along this line. In his book Timaeus, Plato (428/29348/47 B.C.) gives his view of how the world is made up in terms of right-angled triangels. Werner Heisenberg, who was equally fascinated with and puzzeled by this text summarizes this idea in his book Der Teil und das Ganze []. The general idea is that matter is made up of right-angled triangles which, after being paired to form isosceles triangles or squares, are simply joined together to construct the regular bodies of stereometry: cube, tetrahedron, octahedron and icosahedron. These four solids then represent the basic units of the four elements: earth, fire, air and water. Plato makes no statement about the size of the triangles, only about their form and resulting properties.
Some 2000 years later, the idea of Platonic solids (polyhedra) fascinated Johannes Kepler (15711630) so much that, in his quest for harmony in nature, he tried to explain the orbits of the planets in our solar system by fitting one polyhedron onto another so that the radii of spheres enveloping these polyhedra would correspond to the mean distances of the planets from the sun.
An aspect of quantization was brought into this picture by Titius von Wittenberg (17291796) and Johann Elert Bode (17471826) who proposed a series of numbers (integers!) that describes the (relative) distance of the planets from the sun (TitiusBode law) similar to Bohrs model of the atom. (Remarkably, a new formulation of this law has been found by Reinisch ([.
Kepler tried to connect the geometry of the planetary orbits and movement of the planets with some kind of imaginary sounds the music of the spheres. This takes us back to the ancient Greeks and the right-angled triangles.
The Greek philosopher Pythagoras lived around 570500 B.C. Today, even if (almost) nothing survived from our early mathematics lessons, most people can recollect the theorem named after him and some might even be able to quote it as
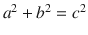
where a and b are the catheti and c the hypotenuse of a right-angled triangle. Pythagoras and his pupils were well-known for their dogma everything is number; number meaning integer . They applied it to develop a musical scale (see Keplers music of the spheres) and also to the right-angled triangle. So, the Pythagorean triples are three integers denoting the length of the three sides of a right-angled triangle thus fulfilling Pythagoras theorem. The most common example is (3, 4, 5) with
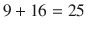
. Asked for a few more examples of this kind, even individuals affiliated with mathematics have difficulty providing some (or even one) though infinitely-many triples exist! Moreover, there is even a rather simple rule to find these triples. This rule, or something similar, was probably already known in Mesopotamia around 2000 B.C. but certainly Diophantus of Alexandria (around the year 250) knew it.
Why do I mention this here? And what does this have to do with the topics stated in the title of this book? In Chap. it is shown that a complex nonlinear evolution equation, in particular a Riccati equation, can be obtained from the dynamics of Gaussian wave packet (WP) solutions of the TD Schrdinger equation (TDSE) that also provides the key to answering the above question of obtaining Pythagorean triples.
Returning to a more recent era of physics, around the beginning of the 20th century, physicists were puzzled by what is called wave-particle duality. For instance light, that (after Maxwell) was finally considered to be a continuous wave, behaved like discrete particles in certain experiments such as the photoelectric effect. Contrarily, electrons that (in the meantime) were assumed to be particles, displayed wave-like behaviour in some experiments and produced interference patterns. The dichotomy of light versus matter, or continuous versus discrete, was only resolved in the mid-twenties of the last century by Schrdinger and Heisenberg (and finally Dirac) with the development of quantum theory [].
Though physically equivalent, Schrdingers wave mechanics turned out to be more successful and receptive to the physics community than Heisenbergs matrix mechanics that used a less familiar mathematical description than Schrdingers partial differential equation. (The Schrdinger picture is also preferred in this book.) As both formulations are closely-related to classical Hamiltonian mechanics, they also have similar properties. In particular, there is no direction of time in the evolution of the system and energy is a constant of motion (at least in the cases that are usually discussed in textbooks and can be solved analytically in closed form).
However, as everyone can observe daily in the surrounding world, nature actually behaves quite differently. There is a direction of time in almost every evolutionary process (and we usually cannot reverse it directly even if we would sometimes like to do so). Also mechanical energy is not a conserved quantity but dissipated into heat by effects like friction. There are ways of explaining and including these phenomena into the theories mentioned earlier. However, for ordinary people, concepts like (Poincars) recurrence time that is longer than the age of the universe are not really convincing. Nevertheless, quantum theory (with all its technological developments) is undoubtedly the most successful theory so far, and not only in physics but also from an economic viewpoint.
The situation in physics took a different twist near the end of the 20th century with the development of Nonlinear Dynamics . This theory is able to describe evolutionary processes like population growth with limited resources or weather patterns and other such complex systems as they occur in real life. At the same time, it can also take into account phenomena like irreversibility of evolution and dissipation of energy.
So why not combine the two theories to get the best of both worlds? In order to answer this question one must specify what the essential elements of these theories are and which aspects can be abandoned in order to have, at least, a chance for unification.












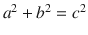 where a and b are the catheti and c the hypotenuse of a right-angled triangle. Pythagoras and his pupils were well-known for their dogma everything is number; number meaning integer . They applied it to develop a musical scale (see Keplers music of the spheres) and also to the right-angled triangle. So, the Pythagorean triples are three integers denoting the length of the three sides of a right-angled triangle thus fulfilling Pythagoras theorem. The most common example is (3, 4, 5) with
where a and b are the catheti and c the hypotenuse of a right-angled triangle. Pythagoras and his pupils were well-known for their dogma everything is number; number meaning integer . They applied it to develop a musical scale (see Keplers music of the spheres) and also to the right-angled triangle. So, the Pythagorean triples are three integers denoting the length of the three sides of a right-angled triangle thus fulfilling Pythagoras theorem. The most common example is (3, 4, 5) with 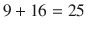 . Asked for a few more examples of this kind, even individuals affiliated with mathematics have difficulty providing some (or even one) though infinitely-many triples exist! Moreover, there is even a rather simple rule to find these triples. This rule, or something similar, was probably already known in Mesopotamia around 2000 B.C. but certainly Diophantus of Alexandria (around the year 250) knew it.
. Asked for a few more examples of this kind, even individuals affiliated with mathematics have difficulty providing some (or even one) though infinitely-many triples exist! Moreover, there is even a rather simple rule to find these triples. This rule, or something similar, was probably already known in Mesopotamia around 2000 B.C. but certainly Diophantus of Alexandria (around the year 250) knew it.