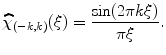Felipe Linares - Introduction to Nonlinear Dispersive Equations
Here you can read online Felipe Linares - Introduction to Nonlinear Dispersive Equations full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2014, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Introduction to Nonlinear Dispersive Equations
- Author:
- Publisher:Springer
- Genre:
- Year:2014
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Introduction to Nonlinear Dispersive Equations: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Introduction to Nonlinear Dispersive Equations" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This textbook introduces the well-posedness theory for initial-value problems of nonlinear, dispersive partial differential equations, with special focus on two key models, the Kortewegde Vries equation and the nonlinear Schrdinger equation. A concise and self-contained treatment of background material (the Fourier transform, interpolation theory, Sobolev spaces, and the linear Schrdinger equation) prepares the reader to understand the main topics covered: the initial-value problem for the nonlinear Schrdinger equation and the generalized Kortewegde Vries equation, properties of their solutions, and a survey of general classes of nonlinear dispersive equations of physical and mathematical significance. Each chapter ends with an expert account of recent developments and open problems, as well as exercises. The final chapter gives a detailed exposition of local well-posedness for the nonlinear Schrdinger equation, taking the reader to the forefront of recent research.
The second edition of Introduction to Nonlinear Dispersive Equations builds upon the success of the first edition by the addition of updated material on the main topics, an expanded bibliography, and new exercises. Assuming only basic knowledge of complex analysis and integration theory, this book will enable graduate students and researchers to enter this actively developing field.
Felipe Linares: author's other books
Who wrote Introduction to Nonlinear Dispersive Equations? Find out the surname, the name of the author of the book and a list of all author's works by series.













 , denoted by
, denoted by 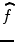 , is defined as:
, is defined as: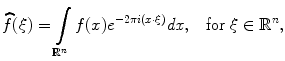
 .
. .
. . Then:
. Then: defines a linear transformation from
defines a linear transformation from 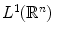 to
to  with
with
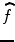 is continuous.
is continuous.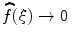 as
as 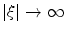 (RiemannLebesgue ).
(RiemannLebesgue ).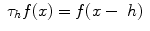 denotes the translation by
denotes the translation by 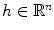 , then
, then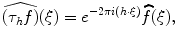
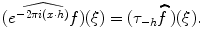
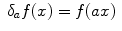 denotes a dilation by
denotes a dilation by 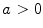 , then
, then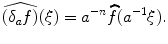
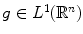 and
and 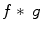 be the convolution of f and g . Then,
be the convolution of f and g . Then,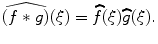
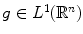 . Then,
. Then,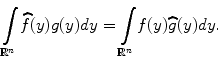
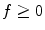 , i.e.,
, i.e., 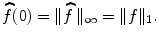
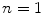 and
and 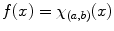 (the characteristic function of the interval
(the characteristic function of the interval 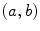 ). Then,
). Then,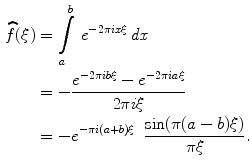
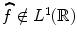 and that
and that 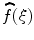 has an analytic extension
has an analytic extension 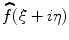 to the whole plane
to the whole plane 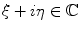 . In particular, if
. In particular, if 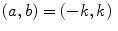 ,
, 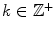 , then we have
, then we have