John P. DAngelo
Department of Mathematics, University of Illinois, Urbana-Champaign, Urbana, IL, USA
ISSN 0743-1643 e-ISSN 2296-505X
Progress in Mathematics
ISBN 978-3-030-75808-0 e-ISBN 978-3-030-75809-7
https://doi.org/10.1007/978-3-030-75809-7
Mathematics Subject Classication (2010): 32M99 32A10 15B57 32V99
The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG 2021
This work is subject to copyright. All rights are solely and exclusively licensed by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This book is published under the imprint Birkhuser, www.birkhauser-science.com by the registered company Springer Nature Switzerland AGThis book is published under the imprint Birkhuser, www.birkhauser-science.com by the registered company Springer Nature Switzerland AG
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
Preface
The unit circle 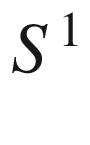 in the complex number system
in the complex number system 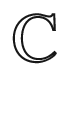 and its self-mappings have played a major role in the history of mathematics. Below we give many striking examples. The central theme throughout this book will be to understand higher dimensional analogues, where things are more subtle and ideas from many fields of mathematics make their appearance.
and its self-mappings have played a major role in the history of mathematics. Below we give many striking examples. The central theme throughout this book will be to understand higher dimensional analogues, where things are more subtle and ideas from many fields of mathematics make their appearance.
In one dimension, if 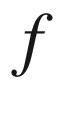 is holomorphic (complex analytic) in a neighborhood of the closure of the unit disk
is holomorphic (complex analytic) in a neighborhood of the closure of the unit disk 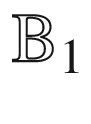 , and
, and 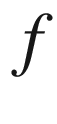 maps the circle to itself, then
maps the circle to itself, then 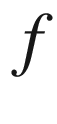 is a finite Blaschke product. One can draw the same conclusion assuming only that
is a finite Blaschke product. One can draw the same conclusion assuming only that 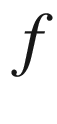 is a proper holomorphic mapping from
is a proper holomorphic mapping from 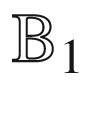 to itself. In particular such functions are rational. Our primary topic will be the study of holomorphic rational maps sending the unit sphere in the source complex Euclidean space
to itself. In particular such functions are rational. Our primary topic will be the study of holomorphic rational maps sending the unit sphere in the source complex Euclidean space  to the unit sphere in some target space
to the unit sphere in some target space  . We call such mappings rational sphere maps. We use the terms monomial sphere map and polynomial sphere map with obvious meaning; even these mappings exhibit remarkably interesting and complicated behavior as the source and target dimensions rise.
. We call such mappings rational sphere maps. We use the terms monomial sphere map and polynomial sphere map with obvious meaning; even these mappings exhibit remarkably interesting and complicated behavior as the source and target dimensions rise.
In this book, a rational sphere map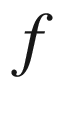 is complex analytic where it is defined. In other words,
is complex analytic where it is defined. In other words, 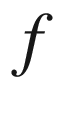 depends on the
depends on the 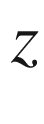 variables but not on the
variables but not on the 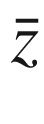 variables. In Chap. we briefly discuss some differences between holomorphic polynomial sphere maps and real polynomial sphere maps. In particular, in complex dimension
variables. In Chap. we briefly discuss some differences between holomorphic polynomial sphere maps and real polynomial sphere maps. In particular, in complex dimension 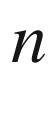 at least
at least  , the only non-constant holomorphic polynomial maps sending the unit sphere to itself are linear, whereas there are real polynomial sphere maps of every degree. I considered the title Complex Analytic Rational Sphere Maps to prevent possible confusion, but the shorter title seems more appealing.
, the only non-constant holomorphic polynomial maps sending the unit sphere to itself are linear, whereas there are real polynomial sphere maps of every degree. I considered the title Complex Analytic Rational Sphere Maps to prevent possible confusion, but the shorter title seems more appealing.
In some sense, this book is a research monograph, as it develops in a systematic fashion most of the research on rational sphere maps done in the last forty years. It differs however from many monographs in several ways, which we now describe.
First of all, scattered throughout the book are a large number of computational examples; the author feels that merging the abstract and concrete enhances both. Many times in his work on this subject, a theorem resulted from trying to cast a collection of examples into one framework. Some readers will stare at these formulas, observe subtle patterns, and pose their own open questions. Other readers may find the formulas distracting. I hope that I have achieved the right balance. Chaps. includes recent code by Lichtblau [1].















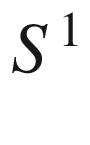 in the complex number system
in the complex number system 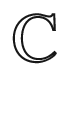 and its self-mappings have played a major role in the history of mathematics. Below we give many striking examples. The central theme throughout this book will be to understand higher dimensional analogues, where things are more subtle and ideas from many fields of mathematics make their appearance.
and its self-mappings have played a major role in the history of mathematics. Below we give many striking examples. The central theme throughout this book will be to understand higher dimensional analogues, where things are more subtle and ideas from many fields of mathematics make their appearance.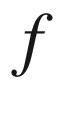 is holomorphic (complex analytic) in a neighborhood of the closure of the unit disk
is holomorphic (complex analytic) in a neighborhood of the closure of the unit disk 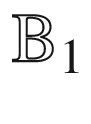 , and
, and 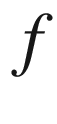 maps the circle to itself, then
maps the circle to itself, then 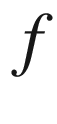 is a finite Blaschke product. One can draw the same conclusion assuming only that
is a finite Blaschke product. One can draw the same conclusion assuming only that 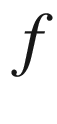 is a proper holomorphic mapping from
is a proper holomorphic mapping from 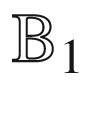 to itself. In particular such functions are rational. Our primary topic will be the study of holomorphic rational maps sending the unit sphere in the source complex Euclidean space
to itself. In particular such functions are rational. Our primary topic will be the study of holomorphic rational maps sending the unit sphere in the source complex Euclidean space  to the unit sphere in some target space
to the unit sphere in some target space  . We call such mappings rational sphere maps. We use the terms monomial sphere map and polynomial sphere map with obvious meaning; even these mappings exhibit remarkably interesting and complicated behavior as the source and target dimensions rise.
. We call such mappings rational sphere maps. We use the terms monomial sphere map and polynomial sphere map with obvious meaning; even these mappings exhibit remarkably interesting and complicated behavior as the source and target dimensions rise.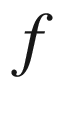 is complex analytic where it is defined. In other words,
is complex analytic where it is defined. In other words, 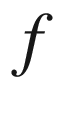 depends on the
depends on the 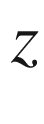 variables but not on the
variables but not on the 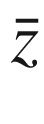 variables. In Chap. we briefly discuss some differences between holomorphic polynomial sphere maps and real polynomial sphere maps. In particular, in complex dimension
variables. In Chap. we briefly discuss some differences between holomorphic polynomial sphere maps and real polynomial sphere maps. In particular, in complex dimension 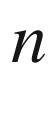 at least
at least  , the only non-constant holomorphic polynomial maps sending the unit sphere to itself are linear, whereas there are real polynomial sphere maps of every degree. I considered the title Complex Analytic Rational Sphere Maps to prevent possible confusion, but the shorter title seems more appealing.
, the only non-constant holomorphic polynomial maps sending the unit sphere to itself are linear, whereas there are real polynomial sphere maps of every degree. I considered the title Complex Analytic Rational Sphere Maps to prevent possible confusion, but the shorter title seems more appealing.