Agustí Reventós Tarrida - Affine Maps, Euclidean Motions and Quadrics
Here you can read online Agustí Reventós Tarrida - Affine Maps, Euclidean Motions and Quadrics full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2011, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Affine Maps, Euclidean Motions and Quadrics
- Author:
- Publisher:Springer
- Genre:
- Year:2011
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Affine Maps, Euclidean Motions and Quadrics: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Affine Maps, Euclidean Motions and Quadrics" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Affine geometry and quadrics are fascinating subjects alone, but they are also important applications of linear algebra. They give a first glimpse into the world of algebraic geometry yet they are equally relevant to a wide range of disciplines such as engineering.
This text discusses and classifies affinities and Euclidean motions culminating in classification results for quadrics. A high level of detail and generality is a key feature unmatched by other books available. Such intricacy makes this a particularly accessible teaching resource as it requires no extra time in deconstructing the authors reasoning. The provision of a large number of exercises with hints will help students to develop their problem solving skills and will also be a useful resource for lecturers when setting work for independent study.
Affinities, Euclidean Motions and Quadrics takes rudimentary, and often taken-for-granted, knowledge and presents it in a new, comprehensive form. Standard and non-standard examples are demonstrated throughout and an appendix provides the reader with a summary of advanced linear algebra facts for quick reference to the text. All factors combined, this is a self-contained book ideal for self-study that is not only foundational but unique in its approach.
This text will be of use to lecturers in linear algebra and its applications to geometry as well as advanced undergraduate and beginning graduate students.
Agustí Reventós Tarrida: author's other books
Who wrote Affine Maps, Euclidean Motions and Quadrics? Find out the surname, the name of the author of the book and a list of all author's works by series.












 together with a map
together with a map 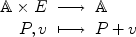
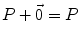 for all
for all 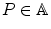 , where
, where 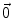 is the identity element of E ;
is the identity element of E ;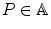 and v , w E ; and
and v , w E ; and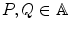 , there exists a unique v E such that P + v = Q .
, there exists a unique v E such that P + v = Q .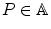 and v E , the notation P + v means only the image of the pair ( P , v ) via the above map
and v E , the notation P + v means only the image of the pair ( P , v ) via the above map 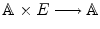 .
.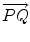 . Hence, we have the fundamental relation
. Hence, we have the fundamental relation 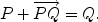
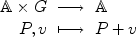
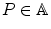 , where e is the identity element of G ; and
, where e is the identity element of G ; and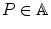 and v , w G ,
and v , w G ,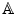 . If, in addition, the following holds:
. If, in addition, the following holds: 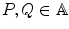 , there exists a unique v G such that P + v = Q ,
, there exists a unique v G such that P + v = Q ,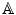 .
.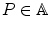 the map
the map 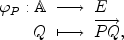
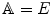 , that is, the points of this affine space are the elements of the vector space. The action is
, that is, the points of this affine space are the elements of the vector space. The action is 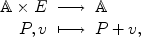
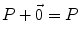 . This is obvious, since
. This is obvious, since