Thomas Lowe - Exploring Scale Symmetry

Exploring Scale Symmetry

Fractals and Dynamics in Mathematics, Science, and the Arts: Theory and Applications

ISSN: 2382-6320

Director

Michel L. Lapidus (University of California, Riverside, CA, USA)

Managing Editors

John A. Rock (California State Polytechnic University, Pomona, CA, USA) &

Machiel van Frankenhuijsen (Utah Valley University, Orem, UT, USA)

Editorial Board

Michael Barnsley (Australian National University, Canberra, Australia)

Valrie Berth (CNRS-Universit Paris Diderot, France)

Robert L. Devaney (Boston University, USA)

Kenneth Falconer (University of St Andrews, Scotland, UK)

Denis Grebenkov (Ecole Polytechnique, France)

Jun Kigami (Kyoto University, Japan)

Jeffrey C. Lagarias (University of Michigan, Ann Arbor, USA)

Ka-Sing Lau (Chinese University of Hong Kong, China)

Heinz-Otto Peitgen (University of Bremen, Germany & Florida Atlantic University, Boca Raton, USA)

Ian Stewart (University of Warwick, England, UK)

Robert S. Strichartz (Cornell University, Ithaca, USA)

Bruce West (Duke University, USA)

Amie Wilkinson (University of Chicago, USA)

Martina Zhle (Friedrich-Schiller University, Jena, Germany)

Published

Vol. 6Exploring Scale Symmetry
by Thomas Lowe

Vol. 5Analysis, Probability and Mathematical Physics on Fractals edited by Patricia Alonso Ruiz (Texas A&M University, USA), Joe P. Chen (Colgate University, USA), Luke G. Rogers (University of Connecticut, USA), Robert S. Strichartz (Cornell University, USA) and Alexander Teplyaev (University of Connecticut, USA)

Vol. 4Quantized Number Theory, Fractal Strings and the Riemann Hypothesis: From Spectral Operators to Phase Transitions and Universality by Hafedh Herichi (Santa Monica College, USA) and Michel L Lapidus (University of California, Riverside, USA)

For the complete list of volumes in this series, please visit
www.worldscientific.com/series/fds

Published by

World Scientific Publishing Co. Pte. Ltd.

5 Toh Tuck Link, Singapore 596224

USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601

UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE

Library of Congress Cataloging-in-Publication Data

Names: Lowe, Thomas, author.

Title: Exploring scale symmetry / Thomas Lowe.

Description: New Jersey : World Scientific, [2021] | Series: Fractals and dynamics in mathematics, science, and the arts: theory and applications, 2382-6320 ; vol. 6 | Includes bibliographical references and index.

Identifiers: LCCN 2020041564 (print) | LCCN 2020041565 (ebook) | ISBN 9789813278547 (hardcover) | ISBN 9789813278554 (ebook) | ISBN 9789813278561 (ebook other)

Subjects: LCSH: Symmetry. | Quantum theory.

Classification: LCC Q172.5.S95 L69 2021 (print) | LCC Q172.5.S95 (ebook) | DDC 516/.1--dc23

LC record available at https://lccn.loc.gov/2020041564

LC ebook record available at https://lccn.loc.gov/2020041565

British Library Cataloguing-in-Publication Data

A catalogue record for this book is available from the British Library.

Copyright 2021 by World Scientific Publishing Co. Pte. Ltd.

All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher.

For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher.

For any available supplementary material, please visit
https://www.worldscientific.com/worldscibooks/10.1142/11219#t=suppl

Desk Editors: George Vasu/Kwong Lai Fun

Typeset by Stallion Press

Email: enquiries@stallionpress.com

Printed in Singapore

For Monica, Maurice and Ollie.

This book is all about the wonderful structures that you can find in the field of scale-symmetric geometry. It is a visual exploration through the less charted regions of this landscape of shapes, searching for extreme and unusual specimens and describing their construction and why they are interesting. Most of all this is a visual book, with lots of images, and graphical descriptions favoured over equations. As such, I expect it to be accessible to mathematicians, programmers, artists and hobbyists alike, though a background in geometry and maths is certainly recommended.

I first began exploring scale-symmetric shapes 10 years ago with help from the online community at fractalforums,1 in this period, I have investigated lots of geometric constructions as a hobby. Some artificial in appearance, some realistic, some animating and some interactive. The common theme is that they are all scale- symmetric, and it is these explorations and findings that I present here. So, this is not a reference book on the current findings in the field, it is instead a description of my own path through this wide and diverse landscape. It follows the process of my exploration of the field, where one idea leads to the next, seeking out only the new, the beautiful and the interesting. Because of this, the majority of examples will be novel and previously uncharacterised. This sits well with the goal of this book: for readers to see what is possible within the field and to use the examples as a stepping stone for their own ideas.

1www.fractalforums.org.

Thomas Lowe works as an Experimental Scientist in the Robotics Group at CSIRO in Australia. He has pursued the topic of scale symmetry for many years, developing several well-known structures, such as the Mandelbox and pyramidal surface fractal. These formulae are popular in the field of fractal art and have been used by special effects studios, such as Luma Pictures, on science fiction and fantasy movies. He has an academic background in computer science and a professional history in 3D computer games and in physically based animation.

The field of geometry has been energised in recent decades by the study of , and how did it become so popular? Lets begin by defining the term as we use it throughout the book.

Visually, it is the symmetry that describes structures such as these:

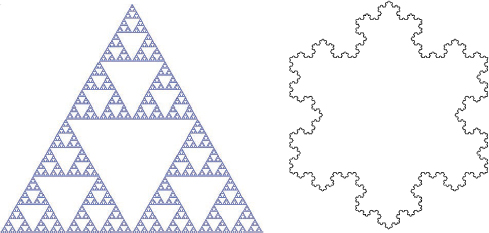
Figure 1. Scale-symmetric structures. Above: .

To get to a definition, lets start by recalling the four elementary symmetries that we learnt at school: