Pierre Berloquin - 100 Geometric Games

Copyright

Copyright 1976 by Pierre Berloquin

All rights reserved.

Bibliographical Note

This Dover edition, first published in 2015, is an unabridged republication of the work originally published by Charles Scribners Sons, New York, in 1976.

Library of Congress Cataloging-in-Publication Data

Berloquin, Pierre.

[100 jeux geometriques. English]

100 geometric games / Pierre Berloquin ; foreword by Martin Gardner ; illustrated by Denis Dugas. Dover edition.

pages cm

Originally published: New York : Charles Scribners Sons, 1976.

eISBN-13: 978-0-486-80567-2

1. Mathematical recreations. 2. GeometryProblems, exercises, etc. I. Title. II. Title: One hundred geometric games.

QA95.B4513 2015

793.74dc23

2015001975

Manufactured in the United States by Courier Corporation
78956X01 2015

www.doverpublications.com

Pierre Berloquin, who put together this stimulating and delightful collection of mind benders, is a clever young Frenchman who was born in 1939 in Tours and graduated in 1962 at the Ecole Nationale Suprieure des Mines in Paris. His training as an operations research engineer gave him an excellent background in mathematics and logical thinking.

But Berloquin was more interested in writing than in working on operations research problems. After two years with a Paris advertising agency, he decided to try his luck at freelance writing and this is how he has earned his living since. In 1964 he began his popular column on Games and Paradoxes in the magazine Science et Vie (Science and Life). Another column, From a Logical Point of View, appears twice monthly in The World of Science, a supplement of the Paris newspaper Le Monde. Occasionally he contributes to other French magazines. One of his favorite avocations is leading groups of crativit, a French cocktail of brainstorming, synectics and encounter therapy, for the discovery of new ideas and the solution of problemsa logical extension of his interest in puzzles.

Berloquins published books are Le Livre des jeux (card and board games), Le jeu de Tarot (Tarot card game), Testez votre intelligence (intelligence tests), 100 grandes russites (solitaire games), Un souvenir denjance dEvariste Galois (Memoir of the Childhood of Evariste Galois), and 100 jeux de cartes classigues (card games); he is co-author of Voulez-vous jouer avec nous (Come Play with Us) and Le livre des divertissements (party games).

This volume is Berloquins own translation into English of one of his four paperback collections of brainteasers which have been enormously popular in France and Italy since they were published in Paris in 1973. This one is concerned only with geometrical puzzles. The other three contain numerical, logical, and alphabetical problems. Denis Dugas, the graphic artist who illustrated all four books, is one of the authors old friends.

The puzzles in this collection have been carefully selected or designed (many are original with the author or artist) so that none will be too difficult for the average reader who is not a mathematician to solve, and at the same time not be too easy. They are all crisply, clearly given, accurately answered at the back of the book, and great fun to work on whether you crack them or not.

At present, Berloquin is living in Neuilly, a Paris suburb, with his wife, Annie, and their two children.

M ARTIN G ARDNER

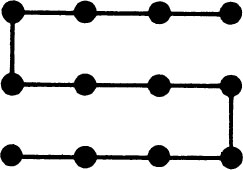
Twelve points are connected above by five straight lines, without raising the pencil.

You can do better: connect the same twelve points:

without raising your pencil

in five straight lines

ending on the first point, thereby making a closed circuit

without going through any point twice (but the lines can cross each other).

How?

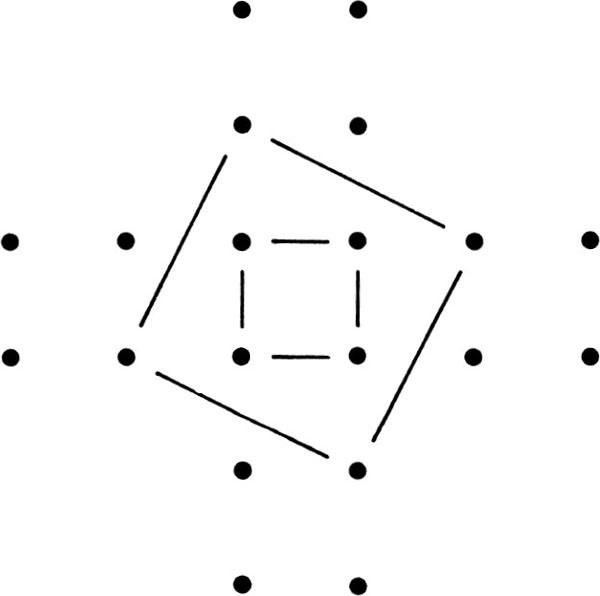
Only two squares are shown out of many squares whose vertexes lie on four of the twenty points in the figure.

How many points do you have to erase so that no square can be formed on any four of the remaining points?

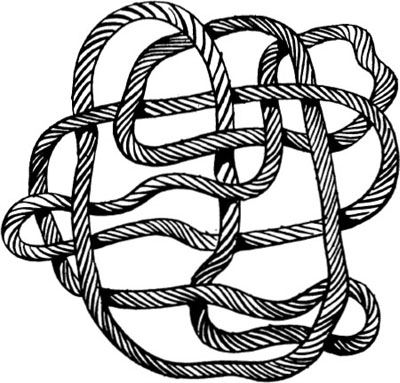
Is the rope a simple loop?

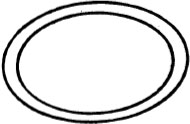
or is it knotted once?

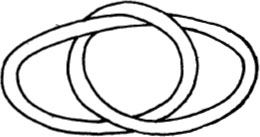
or is it knotted several times?

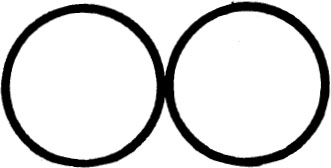
One of two identical coins remains motionless while the other coin rotates around it, touching it without slipping.

When the second coin has completed a turn around the first coin, how many turns has it made around its own axis?

(Solve the problem without using actual coins.)

Go through the maze.

Can you place four chess queens on the board so that none of them threatens another?

(A queen can move any number of squares horizontally, vertically, or diagonally.)

How can you go through the garden:

going along each walk once and only once

without crossing your path

finishing at your starting point?

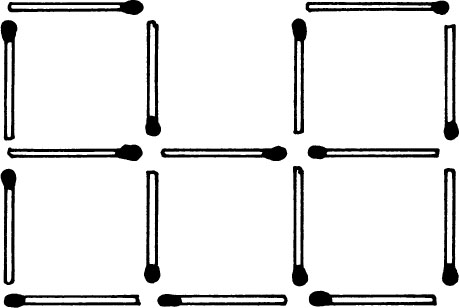
The sixteen matches form five squares. Can you change the position of three matches so that only four squares are formed by the sixteen matches?

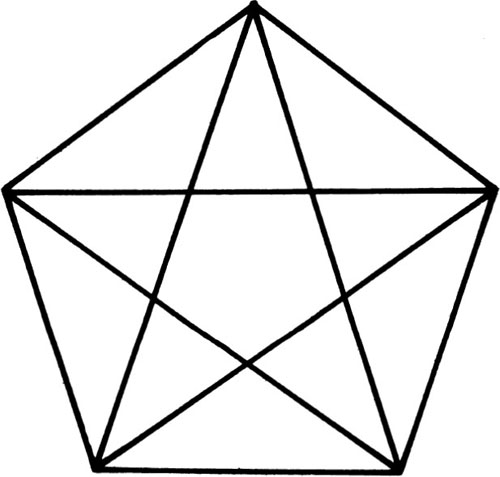
How many triangles are there in the diagram? Can you count them methodically enough not to miss any?