Paul DuChateau - Advanced Mathematics for Engineers and Scientists
Here you can read online Paul DuChateau - Advanced Mathematics for Engineers and Scientists full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2012, publisher: INscribe Digital, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Advanced Mathematics for Engineers and Scientists
- Author:
- Publisher:INscribe Digital
- Genre:
- Year:2012
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
- 100
- 1
- 2
- 3
- 4
- 5
Advanced Mathematics for Engineers and Scientists: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Advanced Mathematics for Engineers and Scientists" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Advanced Mathematics for Engineers and Scientists — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Advanced Mathematics for Engineers and Scientists" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:

THE PHILOSOPHY OF MATHEMATICS: AN INTRODUCTORY ESSAY, Stephan Krner (048647185-3)
COMPANION TO CONCRETE MATHEMATICS: MATHEMATICAL TECHNIQUES AND VARIOUS APPLICATIONS, Z. A. Melzak (048645781-8)
NUMBER SYSTEMS AND THE FOUNDATIONS OF ANALYSIS, Elliott Mendelson. (0486-45792-3)
EXPERIMENTAL STATISTICS, Mary Gibbons Natrella. (0486439372)
AN INTRODUCTION TO IDENTIFICATION, J. P. Norton. (048646935-2)
BEYOND GEOMETRY: CLASSIC PAPERS FROM RIEMANN TO EINSTEIN, Edited with an Introduction and Notes by Peter Pesic. (0-486-45350-2)
THE STANFORD MATHEMATICS Problem BOOK: WITH HINTS AND SOLUTIONS, G. Polya and J. Kilpatrick. (0-486-46924-7)
SPLINES AND VARIATIONAL METHODS, P. M. Prenter. (0-486-46902-6)
PROBABILITY THEORY, A. Renyi. (0-486-45867-9)
LOGIC FOR MATHEMATICIANS, J. Barkley Rosser. (0-486-46898-4)
PARTIAL DIFFERENTIAL EQUATIONS: SOURCES AND SOLUTIONS, Arthur David Snider. (0-486-45340-5)
INTRODUCTION TO BIOSTATISTICS: SECOND EDITION, Robert R. Sokal and F. James Rohlf. (0-486-46961-1)
MATHEMATICAL PROGRAMMING, Steven Vajda. (0-486-47213-2)
THE LOGIC OF CHANCE, John Venn. (0-486-45055-4)
THE CONCEPT OF A RIEMANN SURFACE, Hermann Weyl. (0-486-47004-0)
INTRODUCTION TO PROJECTIVE GEOMETRY, C. R. Wylie, Jr. (0-486-46895-X)
FOUNDATIONS OF GEOMETRY, C. R. Wylie, Jr. (0-486-47214-0)
T his chapter provides an introduction to the solution of systems of linear algebraic equations. After a brief discussion of matrix notation we present the Gaussian elimination algorithm for solving linear systems. We also show how the algorithm can be extended slightly to provide the so-called LU factorization of the coefficient matrix. This factorization is nearly equivalent to computing the matrix inverse and is an extremely effective solution approach for certain kinds of problems. The solved problems provide simple BASIC computer programs for both the Gaussian elimination algorithm and the LU decomposition. These are applied to example problems to illustrate their use. The solved problems also include examples of physical problems for which the mathematical models lead to systems of linear equations.
The presentation of the solution algorithms is rather formal, particularly with respect to explaining what happens when the algorithms fail in the case of a singular system of equations. To provide a clearer understanding of these and other matters we include a brief development of some abstract ideas from linear algebra. We introduce the four fundamental subspaces associated with a matrix A: the row and column spaces, the null space and the range of A. The relationships that exist between these subspaces and the corresponding subspaces for the transpose matrix A T provide the key to understanding the solution of systems of linear equations in the singular as well as the nonsingular case. The solved problems expand on the ideas set forth in the text. For example, Problem 1.15 gives a physical interpretation for the abstract solvability condition that must be imposed on the data vector in a singular system. Problems 1.16 through 1.20 discuss the notion of a least squares solution for an overdetermined system and apply this to least squares fits for experimental data.
We should perhaps conclude this introduction with the disclaimer that this chapter is meant to be only an introduction to the numerical and abstract aspects of systems of linear algebraic equations. While the Gaussian elimination algorithm does form the core of many of the more sophisticated solution algorithms for linear systems, the version provided here contains none of the enhancements that exist to take advantage of special matrix structure, nor does it contain provisions to compensate for numerical instabilities in the system. Such considerations are properly the subject of a more advanced course on numerical linear algebra. This chapter seeks only to provide the foundation on which more advanced treatments can build.(1.1)
Consider the following system of m equations in the n unknowns
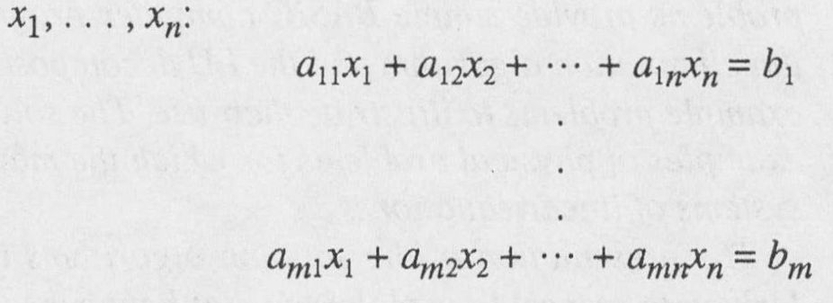
(1.1)
Here a 11, ... , a mn denote the coefficients in the equations and the numbers b 1 ... , b m are referred to as the data. In a specific example these quantities would be given numerical values and we would then be concerned with finding values for x ,... , x n such that these equations were satisfied. An n -tuple of real values { x 1,... , x n } which satisfies each of the m equations in (1.1) is said to be a solution for the system. The collection of all n -tuples which are solutions is called the solution set for the system. For any given system, one of the following three possibilities must occur:
- The solution set contains a single n -tuple; then the system is said to be nonsingular.
- The solution set contains infinitely many n -tuples; then the system is said to be singular, or, more precisely, singular dependent or underdetermined.
- The solution set is empty; in this case we say the system is singular inconsistent or overdetermined.
- Consider the system
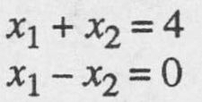
Each equation in this simple system defines a separate function whose graph is a straight line in the x 1 x 2 plane. The lines corresponding to these equations are seen to intersect at the unique point (2, 2). Thus, the solution set for this system consists of the single 2-tuple [2, 2]. The system is nonsingular.
- The system produces just a single line in the x 1 x 2 plane (alternatively, there are two lines that coincide). The solution set for the system contains infinitely many 2-tuples corresponding to all of the points on the line. That is, every 2-tuple that is of the form [ x 1, 2 x 1] for any choice of x 1 is in the solution set. The system is singular. More precisely, the system is singular dependent (underdetermined). The equations of the system are not independent equations.
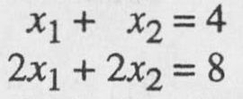
- The system produces a pair of parallel lines in the x 1 x 2 plane. There are no points that lie on both lines and consequently the solution set for the system is empty. The system is singular. More precisely, the system is singular inconsistent (overdetermined). The equations of the system are contradictory.
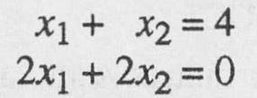
In order to discuss systems of equations efficiently it will be convenient to have the notion of an n-vector. We shall use the notation X to denote an array of n numbers arranged in a column, and X T will denote the same array arranged in a row,
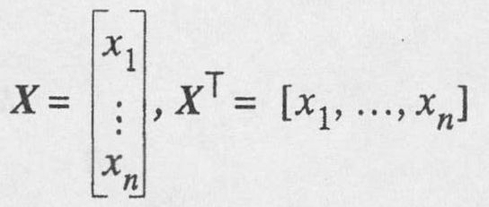
Font size:
Interval:
Bookmark:
Similar books «Advanced Mathematics for Engineers and Scientists»
Look at similar books to Advanced Mathematics for Engineers and Scientists. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Advanced Mathematics for Engineers and Scientists and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.











