C. G. Lambe - Differential Equations for Engineers and Scientists

C. G. LAMBE & C. J. TRANTER DOVER PUBLICATIONS, INC. Mineola, New York Bibliographical Note This Dover edition, first published in 2018, is an unabridged republication of the work originally published by the English Universities Press, Ltd., London, in 1961.

The General Editors Foreword by Sir Graham Sutton from the original edition has been omitted. International Standard Book Number ISBN-13: 978-0-486-82408-6 ISBN-10: 0-486-82408-X Manufactured in the United States by LSC Communications 82408X01 2018 www.doverpublications.com

THE study of ordinary and partial differential equations is an essential part of the training of engineers and scientists and this book is primarily designed for students reading for a first degree in those subjects. The authors have endeavoured to provide a text which covers the elementary theory of differential equations with emphasis on the application of the methods of solution to practical problems. More advanced analytical and numerical techniques are also introduced in so far as they have a bearing on modern scientific theory. Nearly nine hundred worked examples and exercises, with answers, are included. The first four chapters are mainly concerned with the solution of first order equations, linear equations with constant coefficients and simultaneous equations.

In the next two chapters the method of solution by infinite series is followed by an account of the more important special functions of mathematical physics. Partial differential equations are treated in and solutions of Laplaces and other equations are obtained in terms of the special functions, while in the following chapter the method of integral transforms is discussed and applied to the solution of ordinary and partial equations. The next two chapters deal with methods of obtaining approximate solutions by graphical and numerical processes and by the method of relaxation. The final chapter is an introduction to the important modern theory of non-linear differential equations. The authors wish to express their special thanks to their colleague, Dr. N. N.

Everitt, who read the manuscript with great care and made many valuable suggestions. They are also grateful to the Senate of the University of London and the Department of Engineering, Cambridge, for permission to use examination questions, and to the editor and publishers of the Philosophical Magazine for allowing them to reproduce . C. G. LAMBE C. J.

TRANTER Royal Military College of ScienceShrivenham1961

Introduction. Definitions. Formation of differential equations. Elimination of constants. Taylor series expansion of solutions. The differential equation y(n) = f(x).

Exact equations. Introductory. Equations with variables separable. Applications of equations with separable variables. The linear first order differential equation. Bernoullis equation.

Applications of the linear first order equation. Homogeneous equations. Reducible equations. Nonlinear equations of the first order. Clairauts equation. Singular solutions.

Orthogonal trajectories. Riccatis equation. Introductory. Nature of the solutions of linear equations. Solution of reduced second order equations. Solution of reduced nth order equations.

Particular integrals of second order equations. Particular integrals of equations of higher order. Use of operators to find particular integrals. Other methods of finding particular integrals. The Euler linear equation. The vibration equation.

Applications to the theory of structures. Application to electric circuits. Application to servomechanisms. Introductory. Simultaneous equations of the first order. Simultaneous equations of higher orders.

Applications of simultaneous equations. Small oscillations and normal modes. Reducible equations. Introduction. Ordinary and singular points of a differential equation. The indicial equation.

Solutions for large values of x. The Gamma and Beta functions. The convergence of series solutions. The relation between the two solutions of a second order linear equation. The hypergeometric equation. Some properties of the hypergeometric function.

Introduction. Legendres equation. Some properties of Legendre polynomials. Legendres associated equation. Bessels equation. Bessel functions of order zero.

Bessel functions of integral order. Hankel functions. Some properties of Bessel functions. Modified Bessel functions. The ber and bei functions. Some transformations of Bessels equation.

The confluent hypergeometric equation. The Jacobi polynomials. The Gegenbauer polynomials. The Tchebichef polynomials. The Laguerre polynomials. The associated Laguerre polynomials.

The Hermite polynomials. Introduction. Solution by separation of variables. Some practical applications. The equations of mathematical physics. The physical significance of 2V.

Transformation of coordinates. Some solutions of partial differential equations in polar coordinates. Maxwells equations. Schrdingers equation. Introduction. The Laplace transform.

The solution of ordinary differential equations by the Laplace transform. Fouriers integral formula. Fourier transforms and their inversion formulae. The Hankel transform and its inversion formula. Fourier and Hankel transforms of derivatives. The solution of partial differential equations by integral transforms.

Finite transforms. The solution of partial differential equations by finite transforms. Other transforms. Introductory. The method of isoclinals. Phase-plane diagrams.

Numerical solutions of first order equations. Initiation of a solution by Taylors series. Picards method. Eulers method. Runge-Kutta formulae. Finite differences.

Adams-Bashforth formulae. Use of Simpsons rule. Milnes method. Deferred approach to a limit. Simultaneous differential equations. Second order differential equations.

Other methods for second order equations. High-speed electronic computors. Introduction. The solution of ordinary differential equations. Some practical hints. Devices for speeding up the relaxation process.

The completion of the liquidation process. Cases in which the derivative is specified at an end of the range. Extension to other differential equations. Extension to partial differential equations. Block relaxation in two-dimensional problems. Lines of symmetry.

Local effects. Curved boundaries. Extension to other partial differential equations. A physical interpretation of the relaxation method. Introductory. Non-linear equations which are integrable.

Jacobian elliptic functions. Equations integrable in terms of elliptic functions. The equation 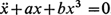. The equation 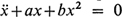. The equation 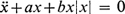. Damped oscillations.

Use of the phase-plane diagram. Van der Pols equation. The method of perturbations. Forced oscillations.

Most problems in science and engineering have to be idealized before their solution can be attempted. This idealization is generally necessary to bring the problem into a form capable of solution by known mathematical techniques, but it is essential, of course, that the actual and idealized problems should bear a close resemblance to one another.