CHAPTER 1 INTRODUCTION In ordinary thermodynamics, thermodynamic functions are defined and mathematical interrelations between these functions are derived for macroscopic (strictly, infinite) systems only. Our main object in this book is to extend the range of validity of these definitions and interrelations to include small, nonmacroscopic systems (e.g., a single macromolecule or colloidal particle). Let us turn immediately to a simple illustration. Suppose a certain one-component macroscopic solid has a Gibbs free energy F = Nf(p, T) where N = number of molecules in the sample and f is a function of p and T only. Several typical interrelations between thermodynamic functions are then 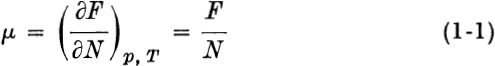 and
and 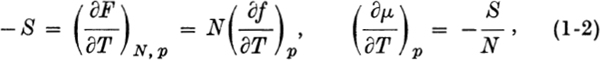 where = chemical potential and S = entropy. Now consider a colloidal particle of the same solid, small enough that correction terms must be added to F.
where = chemical potential and S = entropy. Now consider a colloidal particle of the same solid, small enough that correction terms must be added to F.
For example, suppose  The term in N2/3 is a surface free energy, while the last two terms might be due, among other things, to rotation of the colloidal particle. In the limit N , FNf, the macroscopic relationship.,
The term in N2/3 is a surface free energy, while the last two terms might be due, among other things, to rotation of the colloidal particle. In the limit N , FNf, the macroscopic relationship., 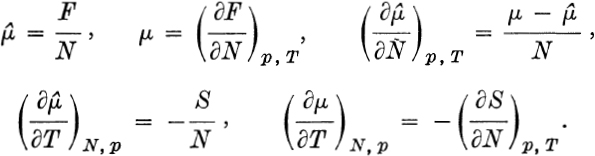 In addition to small terms of order N2/3 and In N, as in , other typical small terms are of order N1/2 (surface of a twodimensional system), N1/3 (second-order surface effect in three dimensions), unity (surface of a one-dimensional system or a small system without surfaces), etc. Small system effects will be particularly noticeable at phase transitions and in critical regions. ENSEMBLE OF SMALL SYSTEMS. Macroscopic thermodynamics will of course apply to a large sample of small systems (e.g., a macro-molecular solution), and macroscopic thermodynamic functions are well defined for such a sample. But we wish to pursue thermodynamics on a smaller scale here: we are interested in thermodynamic functions and interrelationships for a single small system, including, in general, variations in the size of the system (e.g., N, the degree of polymerization or aggregation, F, the volume, etc.).
In addition to small terms of order N2/3 and In N, as in , other typical small terms are of order N1/2 (surface of a twodimensional system), N1/3 (second-order surface effect in three dimensions), unity (surface of a one-dimensional system or a small system without surfaces), etc. Small system effects will be particularly noticeable at phase transitions and in critical regions. ENSEMBLE OF SMALL SYSTEMS. Macroscopic thermodynamics will of course apply to a large sample of small systems (e.g., a macro-molecular solution), and macroscopic thermodynamic functions are well defined for such a sample. But we wish to pursue thermodynamics on a smaller scale here: we are interested in thermodynamic functions and interrelationships for a single small system, including, in general, variations in the size of the system (e.g., N, the degree of polymerization or aggregation, F, the volume, etc.).
Allowance for these variations in size is, indeed, the important new feature which would not be included in a conventional macroscopic thermodynamic treatment of a large sample of small systems where only the number of small systems (macromolecules, etc.) would be varied. will make this particularly clear. Our point of departure in the thermodynamics of small systems will in fact be to start with the macroscopic thermodynamics of a large sample of independent small systems (an ensemble) and introduce N, V, or other such assigned properties of the small systems as variable parameters. The use of an ensemble gives us a firm macroscopic starting point. We shall obtain in this way the desired fundamental thermodynamic equations for a small system. These equations will involve mean values of fluctuating extensive properties (e.g., the energy E).
The mean values will be averages over the ensemble. But experiments will in general be done on ensembles of small systems, so that the ensemble average is just what is required operationally. Conceptually, however, one would like to think as well in terms of time averages for a single small system. For this purpose we have to borrow from statistical mechanics not only the above idea of using an ensemble but also the fundamental postulate that the time average of a property for a single system is equal to the corresponding ensemble average. This is the only new postulate necessary in order to define and use thermodynamic properties for a single small system. Otherwise the foundation of small system thermodynamics is based on macroscopic thermodynamics.
From a strictly operational point of view even this postulate is not necessary if we always understand average to mean ensemble average, not time average. However, the equivalence of these two averages is so well established as a statistical mechanical postulate, for large or small systems, that we shall also adopt the postulate and not make any further distinction between the two averages. There is no need to postulate the equality of ensemble and time averages in ordinary thermodynamics, because, in effect, it suffices for the ensemble to contain only a single (macroscopic) system. APPLICATIONS. As with macroscopic thermodynamics, we may anticipate two main classes of applications of small system thermodynamics: () to verify, stimulate, and provide a framework for statistical mechanical analysis of models of finite (i.e., small) systems. A well-known experimental and theoretical example is the helix-coil transition in synthetic polypeptides.
A single polymer chain is the system in this case. There are very appreciable effects of the degree of polymerization N on intensive properties of the system (e.g., the fraction of helical content). In macroscopic thermodynamics intensive properties are always independent of the size (N here) of a system. For a thermodynamic analysis of such size effects one must therefore turn to small system thermodynamics. An atomic nucleus is a small system of nucleons and an atom is a small system of electrons. Thermodynamics might be of interest for such systems under extreme conditions of temperature.
Experimental small systems, with possible rare exceptions, are condensed , for example). Statistical mechanics is not restricted to macroscopic systems, The applicability of statistical mechanical ensemble theory to small systems as well as large suggests strongly that a parallel thermodynamics should exist. Examples of both the above-mentioned classes of applications, (1) and (2), will be considered in some detail in later chapters. Implicit in the above discussion of applications is the following rather obvious remark, which, however, needs emphasizing. Small system thermodynamics can provide equations, especially differential equations, connecting thermodynamic functions, but the functions themselves must be measured experimentally or calculated from molecular theory (statistical mechanics). The same comment is of course true of macroscopic thermodynamics.
OPERATIONAL DIFFERENCES. There are some important respects in which experimental small thermodynamic systems differ operationally from macroscopic systems, (a) In general, as already mentioned, measurements are not made on a single small system, but on a large number of small systems. An example is a very dilute solution of a macromolecule: the small system is one macromolecule; the solution contains many macromolecules; but the solution must be very dilute so that the systems do not interact with each other, (b) A macroscopic system immersed in a reservoir may exchange heat, molecules, etc., with the reservoir, but the intermolecular interaction between the system and the reservoir at the surface of contact can be neglected in the thermodynamics of the system. This is in general no longer the case for a small system immersed in a solvent (the reservoir). The discussion we give in this introductory chapter does not include solvent effects explicitly. But in solvent effects are present.
All that is required is a reinterpretation of the meaning of various symbols, (c) Certain properties which can be varied at will, experimentally, in a macroscopic system cannot be so varied with a small system. An example is the volume of a colloidal particle. Another is the length of, or mechanical force
Next page
















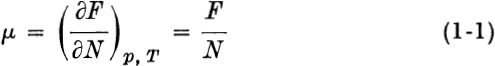 and
and 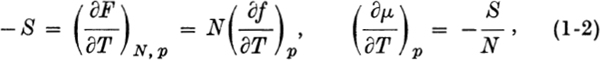 where = chemical potential and S = entropy. Now consider a colloidal particle of the same solid, small enough that correction terms must be added to F.
where = chemical potential and S = entropy. Now consider a colloidal particle of the same solid, small enough that correction terms must be added to F. The term in N2/3 is a surface free energy, while the last two terms might be due, among other things, to rotation of the colloidal particle. In the limit N , FNf, the macroscopic relationship.,
The term in N2/3 is a surface free energy, while the last two terms might be due, among other things, to rotation of the colloidal particle. In the limit N , FNf, the macroscopic relationship., 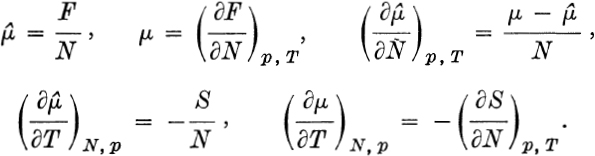 In addition to small terms of order N2/3 and In N, as in , other typical small terms are of order N1/2 (surface of a twodimensional system), N1/3 (second-order surface effect in three dimensions), unity (surface of a one-dimensional system or a small system without surfaces), etc. Small system effects will be particularly noticeable at phase transitions and in critical regions. ENSEMBLE OF SMALL SYSTEMS. Macroscopic thermodynamics will of course apply to a large sample of small systems (e.g., a macro-molecular solution), and macroscopic thermodynamic functions are well defined for such a sample. But we wish to pursue thermodynamics on a smaller scale here: we are interested in thermodynamic functions and interrelationships for a single small system, including, in general, variations in the size of the system (e.g., N, the degree of polymerization or aggregation, F, the volume, etc.).
In addition to small terms of order N2/3 and In N, as in , other typical small terms are of order N1/2 (surface of a twodimensional system), N1/3 (second-order surface effect in three dimensions), unity (surface of a one-dimensional system or a small system without surfaces), etc. Small system effects will be particularly noticeable at phase transitions and in critical regions. ENSEMBLE OF SMALL SYSTEMS. Macroscopic thermodynamics will of course apply to a large sample of small systems (e.g., a macro-molecular solution), and macroscopic thermodynamic functions are well defined for such a sample. But we wish to pursue thermodynamics on a smaller scale here: we are interested in thermodynamic functions and interrelationships for a single small system, including, in general, variations in the size of the system (e.g., N, the degree of polymerization or aggregation, F, the volume, etc.).