LitArk » Books » Home and family

Peter Späth - Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux

Here you can read online Peter Späth - Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2017, publisher: Apress, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Book:
Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux
Author:
Peter Spth
Publisher:
Apress
Genre:
Books / Home and family
Year:
2017
Rating:
3 / 5
Favourites:
Add to favourites
Your mark:
- 60
- 1
- 2
- 3
- 4
- 5

Description
Author's other books
Similar books

Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

Learn how to use Thinking Machine Audio Dreams (ThMAD), a realtime audio visualization engine for Ubuntu Linux. This book bridges the gap between programmers and artists. Both artists and developers with an inclination towards arts will profit from this book since it is a combination of a hands-on tutorial, manual, and reference, with many illustrations that accompany the explanations and tutorials.

Youll learn the basics of ThMADs open source software suite and then start experimenting and building your own rendering pipelines to create audio visualizations. Youll see how to soundly use all ThMADs GUI functionalities, and all modules are provided in a way that will serve both intellectual curiosity and professional needs. The examples that are used as part of the software, and the tutorials included in the book, will serve as a solid basis for your own experiments.

What Youll Learn

Use the ThMAD software, all GUI functionalities, and all modules
Develop your own audio visualization projects
Explore the program operations for ThMAD Artiste and ThMAD Player, including all possible options for controlling program operations.

Who This Book Is For

Visual artists with some IT background, or developers with artistic inclinations. Development experience is not required, but surely helpful.

Peter Späth: author's other books

Who wrote Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux? Find out the surname, the name of the author of the book and a list of all author's works by series.

Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Peter Spth 2017

Peter Spth Audio Visualization Using ThMAD

1. Sound Input

Peter Spth 1

(1)

Leipzig, Germany

In this chapter, we deepen the knowledge of how the computer can be prepared to capture incoming sound or produced sound, how the sound is represented internally, and how the data arrives at ThMAD. We distinguish between the obvious air pressure elongation versus time representation, and the power versus frequency representation, or spectrum .

Preparing for Sound Input

After you purchase a PC or laptop with Ubuntu Linux, or after you have Ubuntu Linux installed on your PC, you have basically two optionsyou can use external audio sources or you can let the sound play from the computer. As for the latter, you could use the CD player of your PC, you could play some files from a USB stick or your hard disk, or you could stream audio files via the Internet or some other means.

Note that other Linux distributions might work as well. Give it a trychances are good that youll find similar programs, tools, and settings to accomplish the same thing.

If you want to use external audio sources, you need a microphone or a sound card with a line-in to connect to. Especially for laptops, the built-in microphones are not of the highest quality, but they might be enough for your purposes. You actually dont want to accurately reproduce the sound, but react to it, and for this aim, having perfectly linear input curves is not too important. On the other hand, if you dont want to lose important impulses from the basses, which can happen with cheap microphones, getting yourself a decent microphone might help you avoid surprises. Also, bear in mind that audio visualizations might be brittle to the structure of the incoming sound under certain circumstances.

Usually you want to avoid that and the overall outcome should be interesting for any kind of music input. This is easy enough to check with different recordings. But if, for example, the basses never make their way through the audio hardware to a suitable extent, because your microphone misses the basses, your rendering pipeline might lack reactiveness to an important part of the incoming sound. If instead for external sound input you just connect some audio source to the line-in jack of your computer, you are automatically on the safe side.

If you want to play CDs using your computers CD player , or play audio files or streamed audio contents, e.g., using your browser, chances are good you dont have to do anything but start suitable programs or let the operating system do it for you automatically. For larger sound file collections, a program for administering them might be handy. RhythmBox, which is preinstalled on Ubuntu, is a good option.

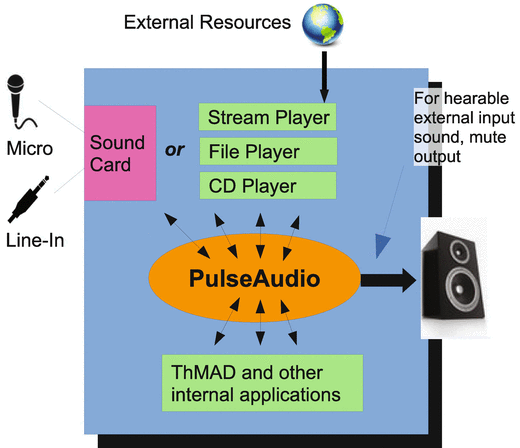
The current version 1.0.0 of ThMAD primarily depends on PulseAudio, which is an audio routing server that handles all sound streams inside your computer. It knows everything thats captured or recorded, and everything thats played. Ubuntu Linux comes with PulseAudio preinstalled and automatically started; for other Linux distributions you may have to install it first.

ThMAD can also connect to ALSA, which is a low-level technology that talks to the sound hardware, and it can connect to JACK, which is a sound server that music professionals usually prefer. It is, however, considerably more difficult to use those options compared to PulseAudio, so we will as a sort of standard case use PulseAudio in the text.

For a graphical description of the standard PulseAudio sound chain, see Figure .

Figure 1-1.

The PulseAudio sound server inside Ubuntu

Understanding Sound Structure

Sound is about air pressure oscillations that are received by your ears. From a mathematical or physical point of view, there are different representations for soundthe time-elongation (or time-pressure) representation and the frequency-power representation. Both of these are discussed in the following sections.

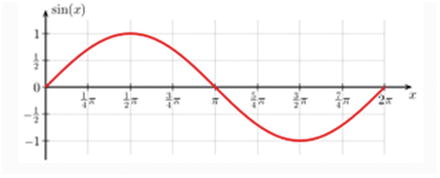
Time-Elongation Representation

On a diagram with the x-axis denoting the time and the y-axis denoting the pressure, the time-elongation representation might, for a sine wave, look like Figure .

Figure 1-2.

A sine wave

In computer systems, we need a digital representation for this sine wave. The idea is as follows: we divide the time into small time steps, say 44,100 steps per second, and for each time step, we write down the current air pressure, or y-value, and save it inside an array. This is sometimes called analog-to-digital conversion (ADC) . Note that 44,100 is a widely adopted industry standard, for example, its used with music CDs. Because we have two ears and like stereo, we do that conversion twice, for the left ear and the right ear. By that means, we end up with 88,200 numbers, which digitally represent one second of stereo sound. For the pressure or y-value representation, we use integer values (-32,768 up to 32,767), with the lower value representing a negative pressure offset, so maybe 0.997 bars, and the higher value representing a positive pressure offset, say 1.003 bars.

According to a scaling we can freely define, these could be mapped to 0.997 bars y=-1000 and 1.003 bars y=+1000. All the other numbers are mean pressures between these values. Of course we could use number ranges other than -32,768 32,767 , but the range we chose here is internally represented by exactly two bytes of data, and computers like that very much. It is also a trade-off: fewer different values means less resolution and poorer quality, and more different values means higher storage need.

Of course, in reality music is stored in lots of different formats, including MP3, Ogg Vorbis and others, mainly for reasons of saving space. The 88,200 numbers per second add up quite rapidly. But in case of letting an application like ThMAD access PulseAudio data, it will receive the data in an uncompressed and untransformed, raw format. This is nice, since then ThMAD doesnt need extra logic to handle different sound formats.

Frequency-Power Representation

A practically less obvious representation of sound consists of writing down the frequency distribution at each instant of time.

Consider the time range [10s;10.1s] when listening to some music. Instead of reporting the air pressure amplitudes at each instant, e.g., 10.000s, 10.001s, 10.002s, we report the frequency mixture of the tones that arrive in our ears during some time range [10s;10.1s]. A 100Hz + b 200Hz + c 300Hz + , where x Hz means a sine oscillation frequency of x per second, and the a, b, c, are weights or power coefficients. The lower the number, the smaller the contribution and the higher, the larger the contribution.

Doing this in a mathematically concise way is called Fourier Transformation , and it turns out that it is a perfectly equivalent way of describing sound. In fact, if we have sound in a pressure versus time representation, we can apply a Fourier Transformation to transfer this into a power versus frequency representation without losing any information. That means the process is reversible and we have something like an Inverse Fourier Transformation to go back the other way. We dont show the mathematical details here; you can find a lot about that in other books and on the Internet.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux»

Look at similar books to Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Robert Ciesla

Sound and Music for Games: The Basics of Digital Audio for Video Games

John S. Tonello

Practical Linux DevOps: Building a Linux Lab for Modern Software Development

David Both

Linux for Small Business Owners: Using Free and Open Source Software to Power Your Dreams

Zac Changnon

Audio Production Basics with Reason Software

Negus Christopher Caen Francois

Ubuntu Linux Toolbox: 1000+ Commands for Ubuntu and Debian Power Users

Dave Mathews [Dave Mathews]

Panda3D 1.6 Game Engine

Larry Bushey

Using Ubuntu MATE and Its Applications: Ubuntu MATE 18.04 LTS Edition

Lechner P.

Multimedia Programming Using Max/MSP and TouchDesigner

Jan Newmarch

Linux Sound Programming

Brian R. Kent

3D Scientific Visualization with Blender

Boris Smus

Web Audio API: Advanced Sound for Games and Interactive Apps

Emilio Raggi

Beginning Ubuntu Linux: Natty Narwhal Edition

Reviews about «Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux»

Discussion, reviews of the book Audio Visualization Using ThMAD: Realtime Graphics Rendering for Ubuntu Linux and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.