Digital
&
Kalman FilteringDigital
&
Kalman FilteringAn Introduction to Discrete-Time Filtering & Optimum Linear Estimation SECOND EDITION S. M. BOZIC DOVER PUBLICATIONS, INC. Mineola, New York Copyright Copyright 1994 by S. M. Bibliographical Note This Dover edition, first published in 2018, is an unabridged republication of the second edition of the work originally printed by Butterworth-Heinemann, United Kingdom, in 1994, and first printed in the United States by Halsted Press, an imprint of John Wiley & Sons, Inc., New York, in 1994. Library of Congress Cataloging-in-Publication Data Names: Bozic, S. M. (Svetozar Mile), author. (Svetozar Mile), author.
Title: Digital and Kalman filtering : an introduction to discrete-time filtering and optimum linear estimation / S.M. Bozic. Description: Second edition, Dover edition [2018 edition]. | Mineola, New York : Dover Publications, 2018. | Second edition originally published: New York : Halsted Press, 1994. | Includes bibliographical references and index.
Identifiers: LCCN 2018017143 | ISBN 9780486817354 | ISBN 0486817350 Subjects: LCSH: Electric filters, Digital. | Kalman filtering. | Signal processing. Classification: LCC TK7872.F5 B7 2018 | DDC 621.3815/324dc23 LC record available at https://lccn.loc.gov/2018017143 Manufactured in the United States by LSC Communications 81735001 2018 www.doverpublications.com ContentsPreface to the first edition The availability of digital computers has stimulated the use of digital signal processing (or time series analysis) in many diverse fields covering engineering and also, for example, medicine and economics. Therefore, the terms digital filtering, Kalman filtering, and other types of processing, appear quite often in the present-day professional literature. The aim of this two-part book is to give a relatively simple introduction to digital and Kalman filtering.
The first part covers a filtering operation as normally understood in electrical engineering and specified in the frequency-domain. The second part deals with the filtering of noisy data in order to extract the signal from noise in an optimum (minimum mean-square error) sense. Digital filtering, as used in the title, refers to of the book, but the subtitle specifies it more closely as an introduction to discrete-time filtering which is a common theory for digital or other types of filter realizations. The actual realization of discrete-time filters, not discussed here, can be done either in sampled-data form (using bucket-brigade or charge coupled devices), or in digital form (using binary logic circuitry). Alternatively, discrete-time filters, described in terms of difference equation algorithms, can be handled on digital computers. Kalman filtering, as used in the title, refers to of the book, and again the subtitle describes it more closely as an introduction to linear estimation theory developed in discrete-time domain.
Although this part deals initially with some digital filter structures, it develops its own terminology. It introduces the criterion of the minimum mean-square error, scalar and vector Wiener and Kalman filtering. However, the main and most practical topic is the Kalman filtering algorithm which in most applications requires the use of digital computers. Most of the material has been used by the author in postgraduate courses over the past five years. The presentation is in tutorial form, but readers are assumed to be familiar with basic circuit theory, statistical averages, and elementary matrices. Various central topics are developed gradually with a number of examples and problems with solutions.
Therefore, the book is suitable both for introductory postgraduate and undergraduate courses. The author wishes to acknowledge helpful discussions with Dr J. A. Edwards of this School, who also helped with some of the computer programs. SMB 1979 Preface to the second edition Over a period of time a number of communications have been received about the first edition of this book. Some were comments about contents and others were corrections regarding the examples and problems.
These have been taken into account in the second edition, and the author wishes to thank all the readers for their contributions. In the second edition some material has been reorganized and some new topics have been added, In , two new sections have been added: circular convolution, and an introduction to multirate digital filters. In has been changed by replacing the vector Wiener filter example with two new examples showing practical aspects in setting up the stage for Kalman filter application. The author wishes to thank referees for their valuable suggestions. It would be nice, in future, to link the examples and problems to the Matlab software package. SMB 1994 Part 1 Digital filteringIntroduction Digital filtering is used here as a well-established title, but with the reservation that we are dealing only with time sequences of sampled-data signals.
However, the fundamental theory presented for discrete-time signals is general and can also be applied to digital filtering. It is important to clarify the terminology used here and in the general field of signal processing. The analogue or continuous-time signal means a signal continuous in both time and amplitude. However, the term continuous-time implies only that the independent variable takes on a continuous range of values, but the amplitude is not necessarily restricted to a finite set of values, as discussed by Rabiner (1). Discrete-time implies that signals are defined only for discrete values of time, i.e. time is quantized.
Such discrete-time signals are often referred to as sampled-data or analogue sample signals. The widely-used term digital implies that both time and amplitude are quantized. A digital system is therefore one in which a signal is represented as a sequence of numbers which take on only a finite set of values. It is also important to clarify the notation used here. In mathematics the time increments or decrements are denoted by t, but in digital filtering the sampling time interval T is generally used. refer to states; (iii) it is more convenient for handling complicated indices, for example x (N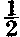 ). refer to states; (iii) it is more convenient for handling complicated indices, for example x (N
). refer to states; (iii) it is more convenient for handling complicated indices, for example x (N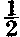 ).
).
It will be seen later that digital filtering consists of taking (usually) equidistant discrete-time samples of a continuous-time function, or values of some discrete-time process, and performing operations such as discrete-time delay, multiplication by a constant and addition to obtain the desired result. The first chapter introduces discrete-time concepts using some simple and familar analogue filters, and also shows how a discrete-time description can arise directly from the type of operation of a system, e. g. radar tracking. The z-transform is then introduced as a compact representation of discrete-time sequences, and also as a link with the Laplace transformation. The second chapter expands the basic concepts established in the first chapter, dealing first with the time response of a discrete-time system (difference equations).
Then we introduce and discuss the transfer function, inversion from z-variable back to time-variable, and the frequency response of a digital filter. This chapter ends with the realization schemes and classification of digital filters into the basic nonrecursive and recursive types, whose design techniques are presented in the third and fourth chapters respectively. In both cases design examples and computer calculated responses are given to illustrate various design methods. In the fifth chapter we return to some of the basic relationships introduced in the first chapter, and deal with two important topics in discrete-time processing. First we develop the discrete Fourier series representation of periodic sequences, which enables formulation of the discrete Fourier transform (DFT) for aperiodic finite sequences. The second topic is the inverse filter, which is an important concept used in many fields for removal or reduction of undesirable parts of a sequence.
Next page










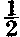 ). refer to states; (iii) it is more convenient for handling complicated indices, for example x (N
). refer to states; (iii) it is more convenient for handling complicated indices, for example x (N