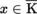Fundamentals of Advanced Mathematics 3
Differential Calculus, Tensor Calculus, Differential Geometry, Global Analysis
Henri Bourls


Copyright
First published 2019 in Great Britain and the United States by ISTE Press Ltd and Elsevier Ltd
Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address:
ISTE Press Ltd
27-37 St Georges Road
London SW19 4EU
UK
www.iste.co.uk
Elsevier Ltd
The Boulevard, Langford Lane
Kidlington, Oxford, OX5 1GB
UK
www.elsevier.com
Notices
Knowledge and best practice in this field are constantly changing. As new research and experience broaden our understanding, changes in research methods, professional practices, or medical treatment may become necessary.
Practitioners and researchers must always rely on their own experience and knowledge in evaluating and using any information, methods, compounds, or experiments described herein. In using such information or methods they should be mindful of their own safety and the safety of others, including parties for whom they have a professional responsibility.
To the fullest extent of the law, neither the Publisher nor the authors, contributors, or editors, assume any liability for any injury and/or damage to persons or property as a matter of products liability, negligence or otherwise, or from any use or operation of any methods, products, instructions, or ideas contained in the material herein.
For information on all our publications visit our website at http://store.elsevier.com/
ISTE Press Ltd 2019
The rights of Henri Bourls to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988.
British Library Cataloguing-in-Publication Data
A CIP record for this book is available from the British Library
Library of Congress Cataloging in Publication Data
A catalog record for this book is available from the Library of Congress
ISBN 978-1-78548-250-2
Printed and bound in the UK and US
Preface
Henri Bourls June 2019
This third volume of of this third volume. Nonetheless, we will need to consider a few generalizations to sketch the so-called convenient context for more recent developments in global analysis; more on this later. We will also present the Carathdory conditions, which are finer than the classical CauchyLipschitz existence and uniqueness conditions for solutions of finite-dimensional ordinary differential equations.
Global questions demand another perspective. Seen through our window, the Earth appears entirely flat, yet even the Greeks in the age of Plato knew better, as testified by an excerpt from his Phaedo (108, e). Knowledge of the Earths shape undoubtedly extended back to the Pythagoreans in the 6th Century BC. Thus, Euclid, who was an avid student of Platos work (consider, for example, his construction of the five Platonic solids in Book XIII of the Elements ), certainly also knew that the Earth is round. Yet his geometry is quite different from the geometry of a sphere. Euclidean geometry offers a good local approximation of spherical geometry but was of course useless for the lengthy voyages of the Renaissance. Global analysis must therefore be expressed in the framework of manifolds , a concept which generalizes curves and surfaces since Riemann.
Ever since the invention of variational calculus in the late 17th Century, it has become common in mathematics to argue about sets of functions. If certain conditions are satisfied, these sets can be endowed with the structure of a manifold, in which case they are called functional manifolds and imagined as deformed versions of the usual function spaces (in the same way that the Earth might be imagined as a deformed version of the plane). Banach manifolds were the first candidates to be considered as a framework for global analysis in the late 1950s and the 1960s [ will demonstrate the considerable value of this approach.
, alongside the theory of differential p -forms.
Our formalism first begins to truly bear fruit in ).
Lie groups are manifolds but also groups; in .
On a reductive Lie group G , we can also fully develop the theory of harmonic analysis (Fourier transforms of functions or tempered distributions). The abelian case will be presented in detail: when G=n  , we recover the usual notion of Fourier transform; when G is the torus Tn
, we recover the usual notion of Fourier transform; when G is the torus Tn 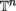 , we recover the Fourier series expansion of periodic functions or distributions. The non-abelian case would fill another entire volume and thus will only be briefly mentioned (even though engineering applications have recently been found ].
, we recover the Fourier series expansion of periodic functions or distributions. The non-abelian case would fill another entire volume and thus will only be briefly mentioned (even though engineering applications have recently been found ].
Defining a geometry on a manifold is equivalent to equipping this manifold with a connection (, Appendix II), who hoped to find a way to unify the theories of gravitation and electromagnetism.
See the Wikipedia article on CoxeterDynkin diagrams.
Errata for Volume 1 and Volume 2
Volume 1 (Contd)
- 1) On p. 12, the fifth line of (V) should read R instead of R .
- 2) On p. 22, on the right-hand side of , it should read lim
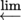 instead of lim
instead of lim 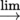 .
. - 3) On p. 41, line 10 should read the cardinal of G / H (equal to the cardinal of G \ H ) instead of this cardinal.
- 4) On p. 45, the first line after should read M 3 instead of G .
- 5) On p. 190, in Definition 3.177, it should read n instead of n .
- 6) On p. 191, in the first line after [3.70], add also denoted as d p after operator.
- 7) On p. 193, line 17 should read Sp
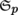 instead of Sn
instead of Sn 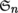 .
. - 8) On p. 220, line 7 should read = j J j where the elementary divisors j are pairwise non-associated and maximal powers (among all elementary divisors) of irreducible polynomials instead of = i = 1 n i .
Volume 2
- 1) On p. 12, line 6 should read K () instead of K ().
- 2) On p. 17, line 19 should read instead of =; line 21 should read does not exist instead of exists.
- 3) On p. 20, line 11 should read 0 i r instead of 1 i r .
- 4) On p. 24, line 28 should read xK
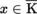











 , we recover the usual notion of Fourier transform; when G is the torus Tn
, we recover the usual notion of Fourier transform; when G is the torus Tn 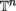 , we recover the Fourier series expansion of periodic functions or distributions. The non-abelian case would fill another entire volume and thus will only be briefly mentioned (even though engineering applications have recently been found ].
, we recover the Fourier series expansion of periodic functions or distributions. The non-abelian case would fill another entire volume and thus will only be briefly mentioned (even though engineering applications have recently been found ].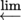 instead of lim
instead of lim 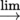 .
.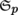 instead of Sn
instead of Sn 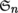 .
.