Charu C. Aggarwal Distinguished Research Staff Member
IBM T.J. Watson Research Center, Yorktown Heights, NY, USA
ISBN 978-3-030-40343-0 e-ISBN 978-3-030-40344-7
https://doi.org/10.1007/978-3-030-40344-7
Springer Nature Switzerland AG 2020
This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This Springer imprint is published by the registered company Springer Nature Switzerland AG
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
Preface
Mathematics is the language with which God wrote the universe. Galileo
A frequent challenge faced by beginners in machine learning is the extensive background required in linear algebra and optimization. One problem is that the existing linear algebra and optimization courses are not specific to machine learning; therefore, one would typically have to complete more course material than is necessary to pick up machine learning. Furthermore, certain types of ideas and tricks from optimization and linear algebra recur more frequently in machine learning than other application-centric settings. Therefore, there is significant value in developing a view of linear algebra and optimization that is better suited to the specific perspective of machine learning.
It is common for machine learning practitioners to pick up missing bits and pieces of linear algebra and optimization via osmosis while studying the solutions to machine learning applications. However, this type of unsystematic approach is unsatisfying, because the primary focus on machine learning gets in the way of learning linear algebra and optimization in a generalizable way across new situations and applications. Therefore, we have inverted the focus in this book, with linear algebra and optimization as the primary topics of interest and solutions to machine learning problems as the applications of this machinery.In other words, the book goes out of its way to teach linear algebra and optimization with machine learning examples. By using this approach, the book focuses on those aspects of linear algebra and optimization that are more relevant to machine learning and also teaches the reader how to apply them in the machine learning context. As a side benefit, the reader will pick up knowledge of several fundamental problems in machine learning. At the end of the process, the reader will become familiar with many of the basic linear-algebra- and optimization-centric algorithms in machine learning. Although the book is not intended to provide exhaustive coverage of machine learning, it serves as a technical starter for the key models and optimization methods in machine learning. Even for seasoned practitioners of machine learning, a systematic introduction to fundamental linear algebra and optimization methodologies can be useful in terms of providing a fresh perspective.
The chapters of the book are organized as follows:
Linear algebra and its applications:The chapters focus on the basics of linear algebra together with their common applications to singular value decomposition, matrix factorization, similarity matrices (kernel methods), and graph analysis. Numerous machine learning applications have been used as examples, such as spectral clustering, kernel-based classification, and outlier detection. The tight integration of linear algebra methods with examples from machine learning differentiates this book from generic volumes on linear algebra. The focus is clearly on the most relevant aspects of linear algebra for machine learning and to teach readers how to apply these concepts.
Optimization and its applications:Much of machine learning is posed as an optimization problem in which we try to maximize the accuracy of regression and classification models. The parent problem of optimization-centric machine learning is least-squares regression. Interestingly, this problem arises in both linear algebra and optimization and is one of the key connecting problems of the two fields. Least-squares regression is also the starting point for support vector machines, logistic regression, and recommender systems. Furthermore, the methods for dimensionality reduction and matrix factorization also require the development of optimization methods. A general view of optimization in computational graphs is discussed together with its applications to backpropagation in neural networks.
This book contains exercises both within the text of the chapter and at the end of the chapter. The exercises within the text of the chapter should be solved as one reads the chapter in order to solidify the concepts. This will lead to slower progress, but a better understanding. For in-chapter exercises, hints for the solution are given in order to help the reader along. The exercises at the end of the chapter are intended to be solved as refreshers after completing the chapter.
Throughout this book, a vector or a multidimensional data point is annotated with a bar, such as 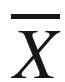 or
or 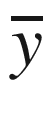 . A vector or multidimensional point may be denoted by either small letters or capital letters, as long as it has a bar. Vector dot products are denoted by centered dots, such as
. A vector or multidimensional point may be denoted by either small letters or capital letters, as long as it has a bar. Vector dot products are denoted by centered dots, such as 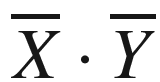 . A matrix is denoted in capital letters without a bar, such asR. Throughout the book, thendmatrix corresponding to the entire training data set is denoted by
. A matrix is denoted in capital letters without a bar, such asR. Throughout the book, thendmatrix corresponding to the entire training data set is denoted by














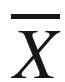 or
or 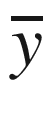 . A vector or multidimensional point may be denoted by either small letters or capital letters, as long as it has a bar. Vector dot products are denoted by centered dots, such as
. A vector or multidimensional point may be denoted by either small letters or capital letters, as long as it has a bar. Vector dot products are denoted by centered dots, such as 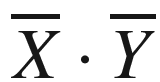 . A matrix is denoted in capital letters without a bar, such asR. Throughout the book, thendmatrix corresponding to the entire training data set is denoted by
. A matrix is denoted in capital letters without a bar, such asR. Throughout the book, thendmatrix corresponding to the entire training data set is denoted by