Boston College - Nano-Optics: Principles Enabling Basic Research and Applications
Here you can read online Boston College - Nano-Optics: Principles Enabling Basic Research and Applications full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Dordrecht;Erice;Italy, year: 2017, publisher: Springer Netherlands, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Nano-Optics: Principles Enabling Basic Research and Applications
- Author:
- Publisher:Springer Netherlands
- Genre:
- Year:2017
- City:Dordrecht;Erice;Italy
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Nano-Optics: Principles Enabling Basic Research and Applications: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Nano-Optics: Principles Enabling Basic Research and Applications" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Note continued: 57. Optical Emission Spectroscopy of Combined Laser Ablation-Hollow Cathode Glow Discharge Plasma Source / Margarita Grozeva -- 58. Femtosecond Transient Absorption Spectroscopy of Photochromic Thiol-Functionalized Terphenylthiazole-Based Diarylethene Molecules / Nataliya Kachalova -- 59. Nanostructural Inhomogeneities in Chalcogenide Glasses Probed by Positron Annihilation Methods / Halyna Klym -- 60. Chiral Plasmonic Core-Shell Nanohelices / L. Kuipers -- 61. Two-Dimensional Dye Self-Assemblies on Graphene: Optical Signature / L. Douillard -- 62.Q-Switching of Ytterbium Lasers by A Graphene Saturable Absorber / Francesc Diaz -- 63. Surface-Enhanced Fluorescence from Polypropylene Substrates / Sergey V. Gaponenko -- 64. Holographic Laser Scanning Microscopy / Antonio Ambrosio -- 65. Physical and Chemical Features of Biochar: A Reservoir of Materials in Advanced Nanotechnologies / F. Miglietta.;Note continued: 39. Luminescent Labeling of Nanoparticles: SiO2@LaPO4 / Andries Meijerink -- 40. Integrated Super-Couplers Based on Zero-Index Metamaterials / Eric Mazur -- 41.3D Micro-printing of Optical Temperature Probes / Martin Wegener -- 42. Evaporation-Driven Aggregation of Nanoparticles in a Free Droplet: Spherical Symmetry in Nanostructured Material / M. Kolwas -- pt. IV Posters -- 43. Ultrafast Optical Spectroscopy Techniques Applied to Colloidal Nanocrystals / Giovanni Bongiovanni -- 44. Directivity Based Nanoscopic Position Sensing / Peter Banzer -- 45.5d-4f Radioluminescence in Pr3+-doped K3YxLu1-x (PO4)2 / M. Bettinelli -- 46. Biosensing on a Chip: Study of Plasmonic Nanostructures Integrated in Microfluidic Devices / Anne-Marie Haghiri-Gosnet -- 47. New Directions in Tip-Enhanced Near-Field Optical Microscopy / Achim Hartschuh -- 48. Phase Singularities in Random Waves: Exploring Optical Statistics at the Nanoscale / L. Kuipers.;Note continued: 13. High-Throughput and Ultra-Sensitive Biosensing and Spectroscopy by Plasmonics / Hatice Altug -- 14. Photoemission from Nanomaterials in Strong Few-Cycle Laser Fields / Matthias F. Kling -- 15. Luminescence of Er3+ Ions in Nanocrystalline Glass-Ceramics / J. Fernandez -- 16. Localization of Yb3+, Er3+ and Co2+ Dopants in an Optical Glass Ceramics of MgAl2O4 Spinel Nano-crystals Embedded in SiO2 Glass / W. Chen -- 17. Nd3+, Eu3+ and Yb3+ Ions as Structural Probes in the Scheelite-Type Cadmium Molybdates with Vacancies / Georges Boulon -- 18. Medical Applications of Nanomaterials / Irene Villa -- 19. Emission Cross Section, Fuchtbauer-Ladenburg Equation, and Purcell Factor / Marc Eichhorn -- 20. Surface Plasmon Enhanced Fluorescence of Glycine-Dimer-Functionalized Silver Nanoparticles / Anatoliy Pinchuk -- pt. II Interdisciplinary Lecture -- 21. Andrea Pozzo: The Art of Perspective / Elpidio Silvestri -- pt. III Short Seminars.;Note continued: 49. Discrimination of Grapevine Genomic DNA Using Surface-Enhanced Raman Spectroscopy and PCA / Nicolae Leopold -- 50. High-Order Multipole Resonances in Cuboidal Surface Phonon Polariton Nanoresonators / J.D. Caldwell -- 51. Polarization Properties of the SERS Radiation Scattered by Linear Nanoantennas with Two Distinct Localized Plasmon Resonances / P.G. Gucciardi -- 52. Fundamental Study and Analytical Applications of Nanoparticle-Enhanced Laser-Induced Breakdown Spectroscopy (NELIBS) of Metals, Semiconductors and Insulators / Alessandro De Giacomo -- 53. New Antibacterial Photoactive Nanocomposite Additives for Endodontic Cements and Fillings / W. Strek -- 54. Low-Loss Phonon Polaritons in Nanostructured Dielectrics / J.D. Caldwell -- 55. Fabrication of SERS Substrates by Roll-to-Roll Hot Embossing / Uli Lemmer -- 56. Coupling Semiconducting Nanowires to Plasmonic Nanoantennas / Gilles Nogues.;Note continued: 22. Effective Oscillator Strengths of Tb3+ Ions in a Garnet Crystal Determined from Low Temperature Magneto-Optic Rotations / Muhammad Sabieh Anwar -- 23. Analysis of Surface Layer Properties of Evaporating Microdroplet of Aqueous SiO2 Nanospheres Suspension with Sodium Dodecyl Sulfate / Krystyna Kolwas -- 24.Compressed Sensing Techniques Applied to the Reconstruction of Magnetic Resonance Images / Francesco Baldacchini -- 25. FDTD Method and HPC for Large-Scale Computational Nanophotonics / Lora Ramunno -- 26. Investigation of the Luminescence Spectral Profiles and the Efficiencies of Yb3+, Nd3+, Tm3+ Doped Y2O3-SiO2 Nano-phosphors / Gonul Eryurek -- 27. Surface Electromagnetic Waves Guided by Non-metallic Interfaces / Muhammad Faryad -- 28. Metal-Enhanced Fluorescence in Plasmonic Waveguides / Denis Boudreau -- 29. Nonlinear Optics in TiO2 Nanoscale Waveguides / Eric Mazur.;Machine generated contents note: pt. I Lectures -- 1. Light-Matter Interactions: A Coupled Oscillator Description / Lukas Novotny -- 2. Luminescence Spectroscopy of Nanophosphors / Baldassare Di Bartolo -- 3. Nanomaterials: Basic Concepts and Quantum Models / Baldassare Di Bartolo -- 4. Non-radiative Processes in Nanocrystals / J.M. Collins -- 5.3D Optical Laser Lithography / Martin Wegener -- 6. Nanostructures and Nanocrystals with Radiation Induced Color Centers: Optical Properties and Applications / Aleksandr P. Voitovich -- 7. Colloidal Nanophotonics: State-of-the-Art and Prospective / Sergey V. Gaponenko -- 8. Ultrafast Nano-Biophotonics / Jean-Pierre Wolf -- 9. Circuit Optomechanics with Diamond Integrated Optical Devices / Wolfram Pernice -- 10. Terahertz Sensing at the Nanoscale / John W. Bowen -- 11. How Latitude Location on a Micro-World Enables Real-Time Nanoparticle Sizing / M.R. Foreman -- 12. Nanoplasmonic and Microfluidic Devices for Biological Sensing / Enzo Di Fabrizio.;Note continued: 66. Modal Behaviour and Switching Properties of a Tailored Parity-Time (PT) Symmetric Grating / B. Maes -- 67. Pulsed Laser-Activated Plasmonic Pyramids for Intracellular Delivery / Eric Mazur -- 68. Multi-resonant Metamaterials for Visible and Near-IR Frequencies / S.M. Prokes -- 69. Nonlinear Properties of Novel Glass-Ceramics with Co2+: Ga2O3 Nanocrystals / Konstantin Yumashev -- 70. Resonant Optical Trapping in Microfluidic-Integrated Hollow Photonic Crystal Cavities / Romuald Houdre -- 71.1-D Photonic Crystals Fabricated by RF Sputtering Towards Photonic Applications / M. Ferraria -- 72. Design of Thin Film Nanocomposite Grating Based Sensors / Ya. Bobitski -- 73. Structure and Luminescence Properties of Nanofluorapatite Activated with Eu3+ Ions Synthesized by Hydrothermal Method / Rafael J. Wiglusz.;Note continued: 30. Mapping the Local Density of States of Periodic Plasmonic Nanostructures with Stochastic Super-resolution / Femius Koenderink -- 31. Design of Optical Nanobiosensors for Detection of Toxic Compounds and Pharmaceutical Products / L. Yotova -- 32. Random Nanocomposites: Fundamental Properties and Application for Harmful Agents Detection / Ivan Karbovnyk -- 33. Hall Effect Sign-inversion and Parallel Hall Effect in Single-constituent 3D Metamaterials / Martin Wegener -- 34.Organization of Metallic Nanoparticles in Block Copolymer Ultra-Thin Films for Optical Devices / Anna Ritcey -- 35. Self-Assembled Laser-Activated Plasmonic Substrates for High-Throughput, High-Efficiency Intracellular Delivery / Eric Mazur -- 36. Single-Crystal vs Polycrystalline Gold: A Non-linear-Optics Analysis / Benoit Cluzel -- 37. Transport of Light Through White-LED Phosphor Plates / W. Vos -- 38. Direct Laser Writing of 3D Nanostructures Using a 405 nm Laser Diode / Martin Wegener.
Boston College: author's other books
Who wrote Nano-Optics: Principles Enabling Basic Research and Applications? Find out the surname, the name of the author of the book and a list of all author's works by series.
Abhay Kumar Singh
Nirmal Mazumder
Juan Carlos Stockert
Federico Capasso
Nielsen
Czymmek Kirk J.
Stig Stenholm
Jacques I. Pankove
Nano-Optics: Principles Enabling Basic Research and Applications — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Nano-Optics: Principles Enabling Basic Research and Applications" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Part I
Lectures
Lectures
Springer Science+Business Media Dordrecht 2017
Baldassare Di Bartolo , John Collins and Luciano Silvestri (eds.) Nano-Optics: Principles Enabling Basic Research and Applications NATO Science for Peace and Security Series B: Physics and Biophysics 10.1007/978-94-024-0850-8_11. Light-Matter Interactions: A Coupled Oscillator Description
Martin Frimmer 1 and Lukas Novotny 1
(1)
Photonics Laboratory, ETH Zrich, 8093 Zrich, Switzerland
Lukas Novotny
Email:
Abstract
The semiclassical theory of light-matter interactions describes the interaction between a classical electromagnetic field with a quantum mechanical two-level system. We show that the quantum mechanical two-level system can be modeled by a system of two coupled classical harmonic oscillators whose eigenstates are split in frequency according to the coupling strength and play the roles of the two levels of the quantum mechanical two-level system. The effect of the light field on the mechanical system is modeled as a modulation of the spring constants of the individual oscillators. Using this fully classical model, we derive the Bloch equations for a two-level system and discuss the mechanical analogues of Rabi oscillations and coherent control experiments.
1.1 Introduction
One of the main thrusts of contemporary physics is quantum engineering, aiming to exploit the properties of quantum systems for information storage, processing and transmission. The fundamental building block of any quantum device is the quantum mechanical two-level system (TLS). In practice, atoms, ions, molecules and solid-state defect centers have been identified as near ideal representations of such a TLS. With the energy-level splittings in these systems corresponding to optical frequencies, light fields provide a handle to control the internal dynamics of such a TLS. To achieve maximum fidelity of the operations on the quantum system, the interaction strength between the electromagnetic field and the TLS has to be maximized by maximizing the field strength at the position of the TLS. Nanophotonics has developed a powerful toolbox to control light at the subwavelength scale, allowing the confinement of electromagnetic radiation to volumes smaller than the limit imposed by diffraction. With the quality factors of nanophotonic resonators increasing, accompanied by shrinking mode volumes, the interaction strength between a single quantum emitter and a nanophotonic resonator is reaching a level where coherent quantum mechanical effects are observable. Various coherent control schemes, such as Rabi oscillations []. However, a classical Newtonian model describing the internal dynamics of a quantum system driven by an external field has been missing to date.
Here, we present a classical model for the interaction of a quantum mechanical TLS with a classical optical field. We construct a mechanical atom , consisting of a pair of coupled classical harmonic oscillators. The coupling gives rise to two eigenmodes, split in frequency according to the strength of the coupling between the bare oscillators. These eigenmodes play the role the two states of a quantum mechanical TLS. The interaction between the mechanical atom and a driving field is reflected in the modulation of the spring constants of the bare oscillators. Under this parametric driving, the Newtonian equations of motion describing the evolution of our mechanical atom take the exact same form as the optical Bloch equations derived from a semiclassical model based on the Schrdinger equation. Accordingly, our model provides as intuitive classical approach to understanding the coherent dynamics of a quantum mechanical TLS.
1.2 Semiclassical Treatment
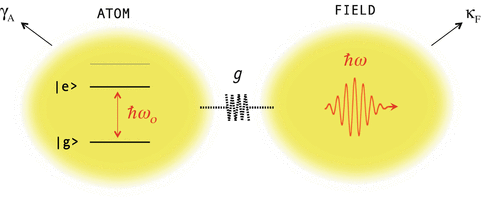
Figure conceptually illustrates the interaction between light and matter in a semiclassical framework. The matter part is described by a TLS, from now on termed atom for simplicity, with an electronic ground state| g and an excited state| e . The two atomic states are separated by the energy 0, with 0 the transition frequency. The spontaneous decay rate of the atom is A . The interaction of the two systems is characterized by the coupling rate g , which derives from the interaction Hamiltonian as g = H int. In the dipole approximation the interaction Hamiltonian can be written as H int= p E , with p denoting the transition dipole between| g and| e . Furthermore, E ( t )= E 0cos t is a classical time-harmonic electric field. Under the influence of the optical field, the wave function of the atom can be written as a superposition of its ground and excited state 
(1.1)
Fig. 1.1
Schematic of light-matter interactions. The optical field is characterized by the frequency and the atom (matter) is represented by two electronic states| g and| e separated by the energy 0. The interaction of the two systems is characterized by the coupling rate g . The excited-state spontaneous decay rate of the atom is A
where a ( t ) and b ( t ) are complex time dependent coefficients. They are found by inserting Eq.( ]) and we only outline the main aspects here. It is convenient to offset the energy scale, such that the energies of ground state and excited state are E g = 02 and E e =+ 02, respectively, and then move to the rotating frame, that is, performing the transformation 
Inserting Eqs.() into the Schrdinger equation and performing the rotating wave approximation (i.e. assuming 0), we obtain 
where we have defined the detuning between the driving frequency and the transition frequency 
and the coupling rate 
(1.2)
(1.3)
(1.4)
(1.5)
which is also denoted as the classical Rabi frequency. Note that the spontaneous decay rate of the atom does not appear in the semiclassical framework and has to be inserted by hand into the equations of motion in ( ]. For our purposes, we neglect spontaneous decay, which places our discussion into the regime of strong driving, where R > A holds for any finite driving field.
Using arbitrary initial conditions 
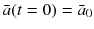
and 
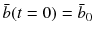
, the solutions of Eq.( ] 
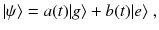
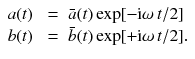
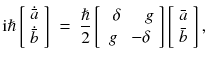
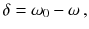
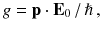
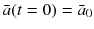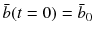and , the solutions of Eq.( ] (1.6)
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Similar books «Nano-Optics: Principles Enabling Basic Research and Applications»
Look at similar books to Nano-Optics: Principles Enabling Basic Research and Applications. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Abhay Kumar Singh
Nirmal Mazumder
Juan Carlos Stockert
Federico Capasso
Nielsen
Czymmek Kirk J.
Stig Stenholm
Jacques I. Pankove
Reviews about «Nano-Optics: Principles Enabling Basic Research and Applications»
Discussion, reviews of the book Nano-Optics: Principles Enabling Basic Research and Applications and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.