1.1 Introduction
Graphs serve as mathematical models to analyze many concrete real-world problems successfully. Certain problems in physics, chemistry, communication science, computer technology, genetics, psychology, sociology, and linguistics can be formulated as problems in graph theory. Also, many branches of mathematics, such as group theory, matrix theory, probability, and topology, have close connections with graph theory.
Some puzzles and several problems of a practical nature have been instrumental in the development of various topics in graph theory. The famous Knigsberg bridge problem has been the inspiration for the development of Eulerian graph theory. The challenging Hamiltonian graph theory has been developed from the Around the World game of Sir William Hamilton. The theory of acyclic graphs was developed for solving problems of electrical networks, and the study of trees was developed for enumerating isomers of organic compounds. The well-known four-color problem formed the very basis for the development of planarity in graph theory and combinatorial topology. Problems of linear programming and operations research (such as maritime traffic problems) can be tackled by the theory of flows in networks. Kirkmans schoolgirl problem and scheduling problems are examples of problems that can be solved by graph colorings. The study of simplicial complexes can be associated with the study of graph theory. Many more such problems can be added to this list.
1.2 Basic Concepts
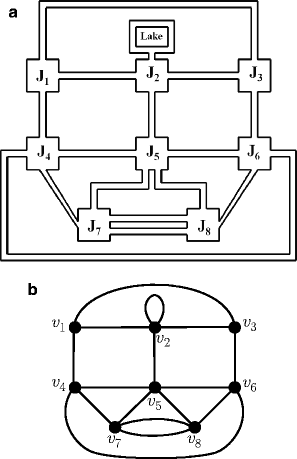
Consider a road network of a town consisting of streets and street intersections. Figure a, there are two streets joining the intersections J 7 and J 8,and there is a loop street starting and ending at J 2.)
Fig. 1.1
( a ) A road network and ( b ) the graph corresponding to the road network in (a)
We now present a formal definition of a graph.
Definition 1.2.1.
A graph is an ordered triple G =( V ( G ), E ( G ), I G ), where V ( G ) is a nonempty set, E ( G ) is a set disjoint from V ( G ),and I G is an incidence relation that associates with each element of E ( G ) an unordered pair of elements (same or distinct) of V ( G ).Elements of V ( G ) are called the vertices (or nodes or points ) of G ,and elements of E ( G ) are called the edges (or lines ) of G . V ( G ) and E ( G ) are the vertex set and edge set of G , respectively. If, for the edge e of G , I G ( e )={ u , v },we write I G ( e )= uv .
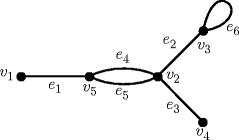
Example 1.2.2.
If V ( G )={ v 1, v 2, v 3, v 4, v 5}, E ( G )={ e 1, e 2, e 3, e 4, e 5, e 6},and I G is given by I G ( e 1)={ v 1, v 5}, I G ( e 2)={ v 2, v 3}, I G ( e 3)={ v 2, v 4}, I G ( e 4)={ v 2, v 5}, I G ( e 5)={ v 2, v 5}, I G ( e 6)={ v 3, v 3},then ( V ( G ), E ( G ), I G ) is a graph.
Diagrammatic Representation of a Graph 1.2.3.
Each graph can be represented by a diagram in the plane. In this diagram, each vertex of the graph is represented by a point, with distinct vertices being represented by distinct points. Each edge is represented by a simple Jordan arc joining two (not necessarily distinct) vertices. The diagrammatic representation of a graph aids in visualizing many concepts related to graphs and the systems of which they are models. In a diagrammatic representation of a graph, it is possible that two edges intersect at a point that is not necessarily a vertex of the graph.
Definition 1.2.4.
If I G ( e )={ u , v },then the vertices u and v are called the end vertices or ends of the edge e .Each edge is said to join its ends; in this case, we say that e is incident with each one of its ends. Also, the vertices u and v are then incident with e .A set of two or more edges of a graph G is called a set of multiple or parallel edges if they have the same pair of distinct ends. If e is an edge with end vertices u and v ,we write e = uv .An edge for which the two ends are the same is called a loop at the common vertex. A vertex u is a neighbor of v in G ,if uv is an edge of G ,and u v .The set of all neighbors of v is the open neighborhood of v or the neighbor set of v ,and is denoted by N ( v );the set N [ v ]= N ( v ) { v } is the closed neighborhood of v in G .When G needs to be made explicit, these open and closed neighborhoods are denoted by N G ( v ) and N G [ v ],respectively. Vertices u and v are adjacent to each other in G if and only if there is an edge of G with u and v as its ends. Two distinct edges e and f are said to be adjacent if and only if they have a common end vertex. A graph is simple if it has no loops and no multiple edges. Thus, for a simple graph G ,the incidence function I G is one-to-one. Hence, an edge of a simple graph is identified with the pair of its ends. A simple graph therefore may be considered as an ordered pair ( V ( G ), E ( G )),where V ( G ) is a nonempty set and E ( G ) is a set of unordered pairs of elements of V ( G ) (each edge of the graph being identified with the pair of its ends).
Example 1.2.5.
In the graph of Fig., edge e 3= v 2 v 4,edges e 4 and e 5 form multiple edges, e 6 is a loop at v 3, N ( v 2)={ v 3, v 4, v 5}, N ( v 3)={ v 2}, N [ v 2]={ v 2, v 3, v 4, v 5},and N [ v 2]= N ( v 2) { v 2}.Further, v 2 and v 5 are adjacent vertices and e 3 and e 4 are adjacent edges.
Fig. 1.2
Graph ( V ( G ), E ( G ), I G ) described in Example
Definition 1.2.6.
A graph is called finite if both V ( G ) and E ( G ) are finite. A graph that is not finite is called an infinite graph. Unless otherwise stated, all graphs considered in this text are finite. Throughout this book, we denote by n ( G ) and m ( G ) the number of vertices and edges of the graph G ,respectively. The number n ( G ) is called the order of G and m ( G ) is the size of G .When explicit reference to the graph G is not needed, V ( G ), E ( G ), n ( G ),and m ( G ) will be denoted simply by V , E , n ,and m ,respectively.
Figure represents a simple graph.
Fig. 1.3
A graph diagram; e 1 is a loop and { e 2, e 3} is a set of multiple edges
Remark 1.2.7.
The representation of graphs on other surfaces such as a sphere, a torus, or a Mbius band could also be considered. Often a diagram of a graph is identified with the graph itself.