Boris Makarov and Anatolii Podkorytov Universitext Real Analysis: Measures, Integrals and Applications 2013 10.1007/978-1-4471-5122-7_1 Springer-Verlag London 2013
1. Measure
Abstract
In this chapter, we give a systematic account of measure theory. The exposition does not assume any preliminary knowledge of the subject. In Sect. , we introduce the notion of measure and establish its basic properties. The next two sections are devoted to the extension of a measure by the Carathodory method and to properties of such an extension. Theorem 1.5.1 on the uniqueness of an extension proved here is repeatedly used in the book.
In Sect. , we study properties of the Borel hull of a system of sets.
1.1 Systems of Sets
In classical analysis, one usually works with functions that depend on one or several numerical variables, but here we will study functions whose argument is a set. Our main focus will be on measures, i.e., set functions that generalize the notions of length, area and volume. Dealing with such generalizations, it is natural to aim at defining a measure on a sufficiently good class of sets. We would like this class to have a number of natural properties, namely, to contain, with any two elements, their union, intersection and set-theoretic difference. In order for a measure to be of interest, its domain must also be sufficiently rich in sets. Aiming to satisfy these requirements, we arrive at the notions of an algebra and a -algebra of sets.
As a synonym for a set of sets, we use the term a system of sets. The sets constituting a system are called its elements. The phrase a set A is contained in a given system of sets
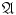
means that A belongs to
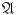
, i.e., A is an element of
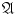
. To avoid notational confusion, we usually denote sets by upper case Latin letters A , B ,, and points belonging to these sets by lower case Latin letters a , b ,. For systems of sets, we use Gothic and calligraphic letters. The symbol stands for the empty set.
1.1.1
We assume that the reader is familiar with the basics of naive set theory. In particular, we leave the proofs of set-theoretic identities as easy exercises. Some of these identities, which will be used especially often, are summarized in the following lemma for the readers convenience.
Lemma
Let A , A () be arbitrary subsets of a set X . Then
Equations (1) and (2) are called De Morgans laws. Equation (3) is the distributive law of intersection over union. Associating union with addition and intersection with multiplication, the reader can easily see the analogy between this property and the usual distributivity for numbers.
Considering the union and intersection of a family of sets with a countable set of indices , we usually assume that the indices are positive integers. This does not affect the generality of our results, since for every numbering of (i.e., every bijection n n from the set of positive integers onto ), we have the equalities
which follow directly from the definition of the union and intersection.
In what follows, we often write a set as the union of pairwise disjoint subsets. Thus it is convenient to introduce the following definition.
Definition
A family of sets { E } is called a partition of a set E if E are pairwise disjoint and E = E .
We do not exclude the case where some elements of a partition coincide with the empty set.
A union of disjoint sets will be called a disjoint union and denoted by . Thus A B stands for the union A B in the case where A B =. Correspondingly, E stands for the union of a family of sets E in the case where all these sets are pairwise disjoint.
We always assume that the system of sets under consideration consists of subsets of a fixed non-empty set, which will be called the ground set. The complement of a set A in the ground set X , i.e., the set-theoretic difference X A , is denoted by A c .
Definition
A system of sets
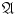
is called symmetric if it contains the complement A c of every element
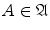
.
Consider the following four properties of a system of sets
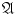
:
( 0)
the union of any two elements of
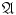
belongs to
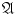
;
( 0)
the intersection of any two elements of
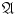
belongs to
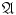
;
()
the union of any sequence of elements of
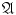
belongs to
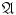
;
()
the intersection of any sequence of elements of
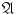
belongs to
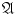
.
The following result holds.
Proposition
If
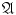
is a symmetric system of sets , then ( 0) is equivalent to ( 0) and () is equivalent to ().
Proof
The proof follows immediately from De Morgans laws. Let us prove, for example, that ()(). Consider an arbitrary sequence { A n } n 1 of elements of
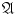
. Their union can be written in the form
Since
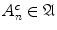
for all n (by the symmetry of
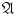
), it follows from () that the intersection of these complements also belongs to
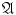
. It remains to use again the symmetry of
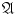
, which implies that
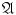














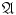 means that A belongs to
means that A belongs to 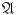 , i.e., A is an element of
, i.e., A is an element of 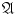 . To avoid notational confusion, we usually denote sets by upper case Latin letters A , B ,, and points belonging to these sets by lower case Latin letters a , b ,. For systems of sets, we use Gothic and calligraphic letters. The symbol stands for the empty set.
. To avoid notational confusion, we usually denote sets by upper case Latin letters A , B ,, and points belonging to these sets by lower case Latin letters a , b ,. For systems of sets, we use Gothic and calligraphic letters. The symbol stands for the empty set.
 is called symmetric if it contains the complement A c of every element
is called symmetric if it contains the complement A c of every element  .
.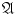 :
: 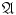 belongs to
belongs to 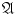 ;
;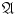 belongs to
belongs to 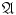 ;
;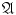 belongs to
belongs to 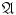 ;
;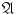 belongs to
belongs to 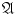 .
.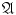 is a symmetric system of sets , then ( 0) is equivalent to ( 0) and () is equivalent to ().
is a symmetric system of sets , then ( 0) is equivalent to ( 0) and () is equivalent to ().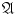 . Their union can be written in the form
. Their union can be written in the form 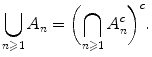
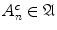 for all n (by the symmetry of
for all n (by the symmetry of 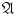 ), it follows from () that the intersection of these complements also belongs to
), it follows from () that the intersection of these complements also belongs to 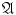 . It remains to use again the symmetry of
. It remains to use again the symmetry of 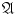 , which implies that
, which implies that