Calculus of Variations I. M. Gelfand S. V. Fomin Translated and Edited by Richard A. Silverman DOVER PUBLICATIONS, INC.
Mineola, New York Copyright Copyright 1963, renewed 1991, by Richard A. Silverman
All rights reserved. Bibliographical Note This Dover edition, first published in 2000, is an unabridged reprint of Calculus of Variations, originally published by Prentice-Hall, Inc., Englewood Cliffs, N.J., in 1963. The translator has made minor corrections to the text for this new edition. Library of Congress Cataloging-in-Publication Data Gelfand, I. (Izrail Moiseevich) [Variatsionnoe ischislenie. (Izrail Moiseevich) [Variatsionnoe ischislenie.
English] Calculus of variations / I.M. Gelfand, S.V. Fomin; translated and edited by Richard A. Silverman. p. cm.
Originally published: Englewood Cliffs, N.J. : Prentice-Hall, 1963. E-ISBN-13: 978-0-486-41448-5 ISBN-10: 0-486-41448-5 (pbk.) 1. Calculus of variations. I. V. (Sergei Vasilevich) II. (Sergei Vasilevich) II.
Silverman, Richard A. III. Title. QA315 .G41713 2000 515.64dc21 00-057099 Manufactured in the United States by Courier Corporation 41448508 www.doverpublications.com AUTHORS PREFACE The present course is based on lectures given by I. M. Gelfand in the Mechanics and Mathematics Department of Moscow State University.
However, the book goes considerably beyond the material actually presented in the lectures. Our aim is to give a treatment of the elements of the calculus of variations in a form which is both easily understandable and sufficiently modern. Considerable attention is devoted to physical applications of variational methods, e.g., canonical equations, variational principles of mechanics and conservation laws. The reader who merely wishes to become familiar with the most basic concepts and methods of the calculus of variations need only study the first chapter. The first three chapters, taken together, form a more comprehensive course on the elements of the calculus of variations, but one which is still quite elementary (involving only necessary conditions for extrema). contains a brief treatment of direct methods in the calculus of variations. contains a brief treatment of direct methods in the calculus of variations.
The authors are grateful to M. A. Yevgrafov and A. G. Kostyuchenko, who read the book in manuscript and made many useful comments. M. G. S. V. F. TRANSLATORS PREFACE This book is a modern introduction to the calculus of variations and certain of its ramifications, and I trust that its fresh and lively point of view will serve to make it a welcome addition to the English-language literature on the subject. TRANSLATORS PREFACE This book is a modern introduction to the calculus of variations and certain of its ramifications, and I trust that its fresh and lively point of view will serve to make it a welcome addition to the English-language literature on the subject.
The present edition is rather different from the Russian original. With the authors consent, I have given free rein to the tendency of any mathematically educated translator to assume the functions of annotator and stylist. In so doing, I have had two special assets: 1) A substantial list of revisions and corrections from Professor S. V. Fomin himself, and 2) A variety of helpful suggestions from Professor J. T.
Schwartz of New York University, who read the entire translation in typescript. The problems appearing at the end of each of the eight chapters and two appendices were made specifically for the English edition, and many of them comment further on the corresponding parts of the text. A variety of Russian sources have played an important role in the synthesis of this material. In particular, I have consulted the textbooks on the calculus of variations by N. I. E. E.
Elsgolts, and by M. A. Lavrentev and L. A. Lyusternik, as well as Volume 2 of the well-known problem collection by N. M.
Gyunter and R. O. Kuzmin, and of G. E. ShilovS Mathematical Analysis, A Special Course. At the end of the book I have added a Bibliography containing suggestions for collateral and supplementary reading.
This list is not intended as an exhaustive catalog of the literature, and is in fact confined to books available in English. R. A. S. CONTENTS , , , , , , , ,
ELEMENTS
OF THE THEORY
1. Functionals.
Some Simple Variational Problems Variable quantities called functionals play an important role in many problems arising in analysis, mechanics, geometry, etc. By a functional, we mean a correspondence which assigns a definite (real) number to each function (or curve) belonging to some class. Thus, one might say that a functional is a kind of function, where the independent variable is itself a function (or curve). The following are examples of functionals: 1. Consider the set of all rectifiable plane curves. A definite number is associated with each such curve, namely, its length.
Thus, the length of a curve is a functional defined on the set of rectifiable curves. 2. Suppose that each rectifiable plane curve is regarded as being made out of some homogeneous material. Then if we associate with each such curve the ordinate of its center of mass, we again obtain a functional. 3. Consider all possible paths joining two given points A and B in the plane.
Suppose that a particle can move along any of these paths, and let the particle have a definite velocity v(x, y) at the point (x, y). Then we obtain a functional by associating with each path the time the particle takes to traverse the path. Then the formula 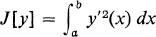 defines a functional on the set of all such functions y(x). 5. As a more general example, let F(x, y, z) be a continuous function of three variables. Then the expression
defines a functional on the set of all such functions y(x). 5. As a more general example, let F(x, y, z) be a continuous function of three variables. Then the expression 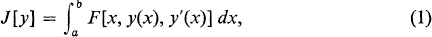 where y(x) ranges over the set of all continuously differentiable functions defined on the interval [a, b], defines a functional.
where y(x) ranges over the set of all continuously differentiable functions defined on the interval [a, b], defines a functional.
By choosing different functions F(x, y, z), we obtain different functionals. For example, if 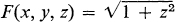 J[y] is the length of the curve y = y(x), as in the first example, while if F(x, y, z) = Z2,J[y] reduces to the case considered in the fourth example. In what follows, we shall be concerned mainly with functionals of the form . Particular instances of problems involving the concept of a functional were considered more than three hundred years ago, and in fact, the first important results in this area are due to Euler (17071783). Nevertheless, up to now, the calculus of functionals still does not have methods of a generality comparable to the methods of classical analysis (i.e., the ordinary calculus of functions). The most developed branch of the calculus of functionals is concerned with finding the maxima and minima of functionals, and is called the calculus of variations.
J[y] is the length of the curve y = y(x), as in the first example, while if F(x, y, z) = Z2,J[y] reduces to the case considered in the fourth example. In what follows, we shall be concerned mainly with functionals of the form . Particular instances of problems involving the concept of a functional were considered more than three hundred years ago, and in fact, the first important results in this area are due to Euler (17071783). Nevertheless, up to now, the calculus of functionals still does not have methods of a generality comparable to the methods of classical analysis (i.e., the ordinary calculus of functions). The most developed branch of the calculus of functionals is concerned with finding the maxima and minima of functionals, and is called the calculus of variations.
Actually, it would be more appropriate to call this subject the calculus of variations in the narrow sense, since the significance of the concept of the variation of a functional is by no means confined to its applications to the problem of determining the extrema of functionals. We now indicate some typical examples of variational problems, by which we mean problems involving the determination of maxima and minima of functionals. 1. Find the shortest plane curve joining two points A and B
Next page












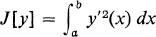 defines a functional on the set of all such functions y(x). 5. As a more general example, let F(x, y, z) be a continuous function of three variables. Then the expression
defines a functional on the set of all such functions y(x). 5. As a more general example, let F(x, y, z) be a continuous function of three variables. Then the expression 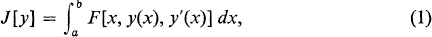 where y(x) ranges over the set of all continuously differentiable functions defined on the interval [a, b], defines a functional.
where y(x) ranges over the set of all continuously differentiable functions defined on the interval [a, b], defines a functional.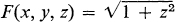 J[y] is the length of the curve y = y(x), as in the first example, while if F(x, y, z) = Z2,J[y] reduces to the case considered in the fourth example. In what follows, we shall be concerned mainly with functionals of the form . Particular instances of problems involving the concept of a functional were considered more than three hundred years ago, and in fact, the first important results in this area are due to Euler (17071783). Nevertheless, up to now, the calculus of functionals still does not have methods of a generality comparable to the methods of classical analysis (i.e., the ordinary calculus of functions). The most developed branch of the calculus of functionals is concerned with finding the maxima and minima of functionals, and is called the calculus of variations.
J[y] is the length of the curve y = y(x), as in the first example, while if F(x, y, z) = Z2,J[y] reduces to the case considered in the fourth example. In what follows, we shall be concerned mainly with functionals of the form . Particular instances of problems involving the concept of a functional were considered more than three hundred years ago, and in fact, the first important results in this area are due to Euler (17071783). Nevertheless, up to now, the calculus of functionals still does not have methods of a generality comparable to the methods of classical analysis (i.e., the ordinary calculus of functions). The most developed branch of the calculus of functionals is concerned with finding the maxima and minima of functionals, and is called the calculus of variations.