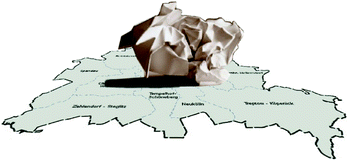
Brouwers fixed-point theorem states that any continuous map from a ball of any dimension to itself has a fixed point. In two dimensions this can be illustrated as follows. Take two identical maps of Berlin or any other ball-shaped city. Now crumple one of the maps as you like and throw it on the other, flat, map as shown in Fig.. Then there exists a location in the city that on the crumpled map is exactly above the same place on the flat map.
Fig. 1.1
A city map twice
For the general formulation of Brouwers theorem, recall that the n -dimensional Euclidean ball is given by all points of distance at most 1 from the origin in n -dimensional Euclidean space, i.e.,
The first proof that we provide for this theorem relies on a beautiful combinatorial lemma that we will discuss in the next section. There also exists a very short and simple proof using homology theory that we present on page .
Sperners Lemma
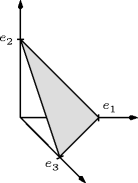
Brouwers fixed-point theorem is intimately related to a combinatorial lemma by Sperner that deals with labelings of triangulations of the simplex. Consider the standard n -simplex given as the convex hull of the standard basis vectors
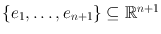
, see Fig.:
Fig. 1.2
The standard 2-simplex
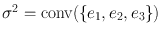
By n we denote the (geometric) simplicial complex given by n and all its faces, i.e.,
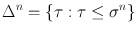
. Assume that K is a subdivision of n . We may think of K as being obtained from n by adding extra vertices. For precise definitions and more details on simplicial complexes we refer to Appendix B. For any n , denote the set {1,, n } by [ n ]. In the definition of a Sperner labeling we will use labels from 1 to n +1, i.e., labels from the set [ n +1].
Definition 1.2.
A Sperner labeling is a labeling
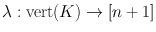
of the vertices of K satisfying
for all v vert( K ).
More intuitively, a Sperner labeling is the following. Consider the minimal face of n that contains v . Say it is given by the convex hull of
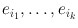
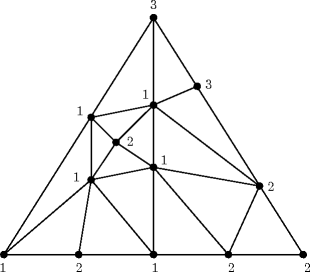
. Then v is allowed to get labels only from { i 1,, i k }. In particular, the vertices e i obtain label i , while a vertex along the edge spanned by e i and e j obtains the label i or j , and so on. For an illustration see Fig..
Fig. 1.3
A Sperner-labeled triangulation of a 2-simplex
Call an n -simplex of Kfully labeled (with respect to ) if its n +1 vertices obtain distinct labels, i.e., if all possible labels from the set [ n +1] appear.
Lemma 1.3 (Sperner []).
Let : vert (K) [ n + 1] be a Sperner labeling of a triangulation K of the n-dimensional simplex. Then there exists a fully labeled n-simplex in K. More precisely, the number of fully labeled n-simplices is odd.
We will now present two inductive proofs of this amazing lemma. The first is a combinatorial construction that constructs one of the desired simplices, while the other is algebraic and uses the concept of a chain complex of a simplicial complex. The inductive proofs reveal a typical phenomenon: while we are mainly interested in the existence of a fully labeled simplex, the induction works only for the stronger statement that there is an odd number of fully labeled simplices.
A third proof, given on page of this section, proves the Sperner lemma as an application of Brouwers fixed-point theorem.
Proof (combinatorial).
The lemma is clearly valid for n =1. Now let n 2 and consider the ( n 1)-dimensional face of n given by the convex hull of e 1,, e n . Note that K restricted to is Sperner labeled with label set [ n ]. We construct a graph as follows. Let the vertex set be all n -simplices of K plus one extra vertex o . The extra vertex o is connected by an edge to all n -simplices that have an ( n 1)-simplex as a face that is labeled with all labels of [ n ] and lies within . Two n -simplices are connected by an edge if and only if they share an ( n 1)-dimensional face labeled with all of [ n ]. See Fig. for an example of the resulting graph.













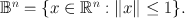
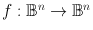 from the n-dimensional ball
from the n-dimensional ball 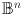 to itself has a fixed point, i.e., there exists an
to itself has a fixed point, i.e., there exists an 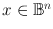 such that f(x) = x.
such that f(x) = x.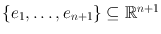 , see Fig.:
, see Fig.: 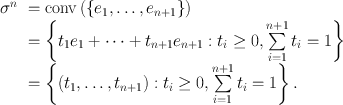
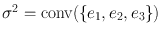
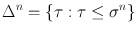 . Assume that K is a subdivision of n . We may think of K as being obtained from n by adding extra vertices. For precise definitions and more details on simplicial complexes we refer to Appendix B. For any n , denote the set {1,, n } by [ n ]. In the definition of a Sperner labeling we will use labels from 1 to n +1, i.e., labels from the set [ n +1].
. Assume that K is a subdivision of n . We may think of K as being obtained from n by adding extra vertices. For precise definitions and more details on simplicial complexes we refer to Appendix B. For any n , denote the set {1,, n } by [ n ]. In the definition of a Sperner labeling we will use labels from 1 to n +1, i.e., labels from the set [ n +1].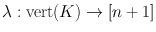 of the vertices of K satisfying
of the vertices of K satisfying 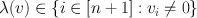
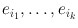 . Then v is allowed to get labels only from { i 1,, i k }. In particular, the vertices e i obtain label i , while a vertex along the edge spanned by e i and e j obtains the label i or j , and so on. For an illustration see Fig..
. Then v is allowed to get labels only from { i 1,, i k }. In particular, the vertices e i obtain label i , while a vertex along the edge spanned by e i and e j obtains the label i or j , and so on. For an illustration see Fig..