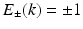Emil Prodan - Bulk and Boundary Invariants for Complex Topological Insulators
Here you can read online Emil Prodan - Bulk and Boundary Invariants for Complex Topological Insulators full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2016, publisher: Springer International Publishing, genre: Science. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Bulk and Boundary Invariants for Complex Topological Insulators
- Author:
- Publisher:Springer International Publishing
- Genre:
- Year:2016
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Bulk and Boundary Invariants for Complex Topological Insulators: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Bulk and Boundary Invariants for Complex Topological Insulators" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This monograph offers an overview of rigorous results on fermionic topological insulators from the complex classes, namely, those without symmetries or with just a chiral symmetry. Particular focus is on the stability of the topological invariants in the presence of strong disorder, on the interplay between the bulk and boundary invariants and on their dependence on magnetic fields.
The first part presents motivating examples and the conjectures put forward by the physics community, together with a brief review of the experimental achievements. The second part develops an operator algebraic approach for the study of disordered topological insulators. This leads naturally to the use of analytical tools from K-theory and non-commutative geometry, such as cyclic cohomology, quantized calculus with Fredholm modules and index pairings. New results include a generalized Streda formula and a proof of the delocalized nature of surface states in topological insulators with non-trivial invariants. The concluding chapter connects the invariants to measurable quantities and thus presents a refined physical characterization of the complex topological insulators.
This book is intended for advanced students in mathematical physics and researchers alike.
Emil Prodan: author's other books
Who wrote Bulk and Boundary Invariants for Complex Topological Insulators? Find out the surname, the name of the author of the book and a list of all author's works by series.









![Eisner Tanja - Operator Theoretic Aspects of Ergodic Theory [recurso electrónico] $c](/uploads/posts/book/173124/thumbs/eisner-tanja-operator-theoretic-aspects-of.jpg)




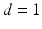
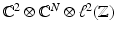 and is given by
and is given by 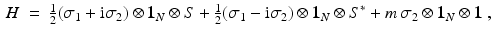
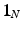 and
and 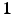 are the identity operators on
are the identity operators on 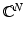 and
and 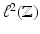 and the
and the 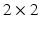 Pauli matrices are
Pauli matrices are 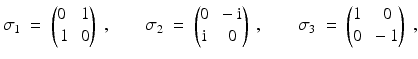
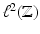 while
while 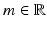 is the mass term. The component
is the mass term. The component 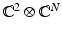 of the Hilbert space will be referred to as the fiber. This Hamiltonian goes back to Su et al. [205] and its physical origin will be discussed in Sect.. It has a chiral symmetry w.r.t. the real unitary
of the Hilbert space will be referred to as the fiber. This Hamiltonian goes back to Su et al. [205] and its physical origin will be discussed in Sect.. It has a chiral symmetry w.r.t. the real unitary 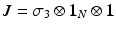 squaring to the identity
squaring to the identity 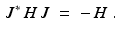
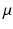 is always assumed positioned at 0 for chiral symmetric systems, see Chap.. Note that a model with chiral symmetry can display a spectral gap at
is always assumed positioned at 0 for chiral symmetric systems, see Chap.. Note that a model with chiral symmetry can display a spectral gap at 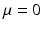 only if the fiber has even dimension, which is obviously the case here.
only if the fiber has even dimension, which is obviously the case here.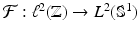 defined by
defined by 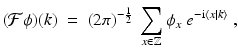
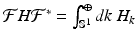 with
with 
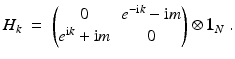
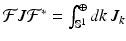 , even with constant fibers
, even with constant fibers  . The two eigenvalues of
. The two eigenvalues of 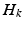 are
are 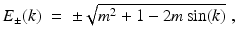
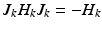 which, as for any Hamiltonian with chiral symmetry, implies
which, as for any Hamiltonian with chiral symmetry, implies 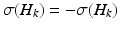 . The central gap around 0 is
. The central gap around 0 is 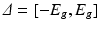 with
with 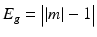 . Hence it is open as long as
. Hence it is open as long as 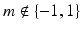 . Let us also note that for
. Let us also note that for 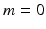 , one has
, one has