DESIGN AND ANALYSIS OF
ALGORITHMS
The Learners Approach
Published by Rashmi V
Version 1.0
Copyright 2020
Author: Rashmi V
Preface
The Author is in teaching field for Computer Science and Engineering colleges. The author tought this subject to the students.
The design and analysis of algorithms is a slightly complex subject as students felt. The author made detailed examples to be understood by the learners through this book.
The author organized the chapters as below.
Chapter 1 gives the overview of algorithms and how to write the pseudocode. It also describes the performance analysis in terms of time complexity and space complexity along with priori and posteriori analysis. This chapter covers the asymptotic notations including Big-Oh, Omega, Theta and Little-Oh notations. It gives instructions about probabilistic and amortized analysis. It is also elaborated on how to solve recurrence relations.
Chapter 2 acquaints the reader with the concepts on representation of sets, types of sets, operations on sets, laws of set theory along with disjoint sets and disjoint set operations. It also includes union and find algorithms with their operations. It covers tree traversal techniques, graph traversal, spanning trees and connected components.
Chapter 3 introduces to the divide and conquer techniques along with their advantages. It covers applications of divide and conquer approach like binary search, finding minimum and maximum, quick sort, merge sort, Stressens matrix multiplication and examples of each application.
Chapter 4 illustrates the greedy method properties along with the comparision with divide and conquer method. It gives the control abstraction of greedy method. Applications of greedy method like job sequencing with deadlines, Knapsack problem, minimum cost spanning trees, single source shortest problem with solved problem.
Chapter 5 deals with dynamic programming. The key elements of dynamic programming, principle of optimality and differences between divide and conquer and greedy method. It discuss about differences of dynamic programming with divide and coquer and greedy method. General characteristics of dynamic programming along with its applications like matrix chain multiplication, optimal binary search trees, 0/1 Knapsack problem, all pairs shortest problem, travelling sales person problem with solved problems are explained.
Chapter 6 briefly covers about the constraints for backtracking. The comparisions between backtracking and brute force approach are explained. The efficiency of backtracking is estimated. The applications of backtracking like n-quuens problem, sum of subsets problem, graph coloring and Hamiltonian cycles are explained with solved problems.
Chapter 7 discusses branch and bound method. The backtracking method and branch and bound method differences are given. It covers the topics about least cost search, bounding, FIFO branch and bound, LIFO branch and bound. The applications of branch and bound method including travelling sales person problem and 0/1 Knapsack problem are explained with the solved problem.
Chapter 8 explains NP-hard and NP-complete problems concepts. The non-deterministic algorithms for sorting and searching are discussed. It also includes decision problem and optimization problem. It discusses about satisfiability, NP-hard and NP- complete classes along with cooks theorem.
I sincerely hope that the readers will be able to make most out of this book.
Good luck!
Table of Contents
OVERVIEW OF ALGORITHMS
1.1 WHAT IS ALGORITHM?
The word algorithm comes from the name of Persial author named Abu Jafar Mohammed Ibn Musa al Khowarizmi who was a mathematician. In mathematics, computer science and related subjects an algorithm is an effective method for solving a problem which is expressed as a finite sequence of steps.
1.1.1 The Definition to Algorithm
An algorithm is typically refers to a set of instructions that can be executed by a computer to produce the desired result.
We can also define algorithm as An algorithm is clearly specified step-by-step process of solving particular problem. An algorithm is a set of rules that must be followed when solving a specific problem.
An algorithm is an efficient method that can be expressed within finite amount of time and space. An algorithm is the best way to represent the solution of a specific problem in a very simple and efficient way. If an algorithm is considered for a specific problem, we can implement it in any programming language, which means that the algorithm is independent from any programming language.
1.1.2 Outline of Algorithm Design
The important aspect of algorithm design include creating an efficient algorithm to solve a particular problem in an efficient way using minimum time and space.
Different approaches can be used to solve a particular problem. Some algorithms can be efficient with respect with time consumption, where as other approaches may be memory efficient. However an algorithm cannot optimize both time consumption and memory usage simultaneously. If we require an algorithm to run in lesser time, more memory must be invested. If we require an algorithm to run with lesser memory, we need to have more time.
1.1.3 Notation of Algorithm
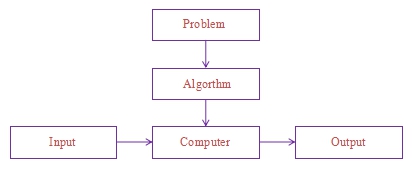
Each algorithm is a module which is designed to handle specific problem relative to particular data structure. The following figure shows the notation of algorithm.
Fig. 1.1.1: Notation of Algorithm
The diagram for notation of algorithm illustrates some of the important points. They are:
1) The non-ambiguity requirement for each step of an algorithm cannot be compromised.
2) The range of inputs for which an algorithm works has to be specified carefully.
3) The same algorithm can be represented in several different ways.
4) Several algorithms for solving the same problem may exist.
5) Algorithms for the same problem can be based on very different ideas and can solve the problem with different speeds.
1.1.4 Properties of Algorithm
According to D. E. Knuth, the algorithm must have the following five properties.
1) Input: An algorithm has zero or more input quantities that are given to it initially before the algorithm begins or dynamically as the algorithm runs. These inputs are taken from specified set of objects. The input refers to the data (facts, figures and numbers) provided to the algorithm on which the computation is performed.
2) Output: An algorithm has one or more outputs that have a specified relation to the inputs.
3) Definiteness: Each step of an algorithm must be precisely defined which means that the actions to be carried out must be rigorously and unambiguously specified for each case. Operations such as compute 7/0 or add 5 or 3 to x are not permitted because it is not clear what the result is or which of the two possibilities should be done.
4) Finiteness: An algorithm must always terminate after a finite number of steps, each of which may require one or more operations. By tracing the instructions of an algorithm and for all cases the algorithm terminates after a finite number of steps.
5) Effectiveness: An algorithm is also generally expected to be effective, in the sense that its operations must all be sufficiently basic and have finite length of time which must be solved by someone using pencil and paper. Performing arithmetic on integers is an example of an effective operation, but arithmetic on real numbers is not because some values may be expressible by infinitely long decimal expansion.






![Magnus Lie Hetland [Magnus Lie Hetland] - Python Algorithms: Mastering Basic Algorithms in the Python Language, Second Edition](/uploads/posts/book/124062/thumbs/magnus-lie-hetland-magnus-lie-hetland-python.jpg)


