Contents
Pagebreaks of the print version

Designs from
Linear Codes
Second Edition
Designs from
Linear Codes
Second Edition
Cunsheng Ding
The Hong Kong University of Science
and Technology, Hong Kong
Chunming Tang
China West Normal University, China

Published by
World Scientific Publishing Co. Pte. Ltd.
5 Toh Tuck Link, Singapore 596224
USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601
UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE
British Library Cataloguing-in-Publication Data
A catalogue record for this book is available from the British Library.
DESIGNS FROM LINEAR CODES
Second Edition
Copyright 2022 by World Scientific Publishing Co. Pte. Ltd.
All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the publisher.
For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher.
ISBN 978-981-125-132-0 (hardcover)
ISBN 978-981-125-133-7 (ebook for institutions)
ISBN 978-981-125-134-4 (ebook for individuals)
For any available supplementary material, please visit
https://www.worldscientific.com/worldscibooks/10.1142/12697#t=suppl
Printed in Singapore
Preface
Since the publication of the first edition of this monograph, the following advances on constructing combinatorial t-designs with linear codes have been made:
A generalization of the Assmus-Mattson theorem for linear codes over finite fields [Tang, Ding and Xiong (2019)].
The discovery of an infinite family of near MDS codes over finite fields supporting an infinite family of 2-designs [Ding and Tang (2020)].
The discovery of an infinite family of BCH codes over GF(22m+1) of length 22m+1 + 1 supporting an infinite family of 4-designs [Tang and Ding (2021)].
These advances are the main motivation for the second edition of this monograph.
The Assmus-Mattson theorem was developed in 1969, and has been used to construct many infinite families of 2-designs and 3-designs in the past 50 years. However, some infinite families of linear codes do support t-designs, but the t-design property of the incidence structures defined by the linear codes cannot be proved with the Assmus-Mattson theorem and the automorphism group of the codes. In the past 50 years, a strengthening of the Assmus-Mattson theorem for special binary linear codes was documented in Calderbank, Delsarte and Sloane (1991) and several analogues of the Assmus-Mattson theorem in other contexts (for example, certain association schemes [Morales and Tanaka (2018)], codes over 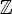 4 [Tanabe (2000)], and rank-metric codes [Byrne and Ravagnani (2019)]) were developed. The Assmus-Mattson theorem for matroids developed in Britz, Royle and Shiromoto (2009) does contain the original Assmus-Mattson theorem as a special case, but it becomes the Assmus-Mattson theorem when it is applied to codes. The generalized Assmus-Mattson theorem for linear codes over finite fields developed in Tang, Ding and Xiong (2019) turns out to be useful, and will be the topic of a new chapter in this second edition.
4 [Tanabe (2000)], and rank-metric codes [Byrne and Ravagnani (2019)]) were developed. The Assmus-Mattson theorem for matroids developed in Britz, Royle and Shiromoto (2009) does contain the original Assmus-Mattson theorem as a special case, but it becomes the Assmus-Mattson theorem when it is applied to codes. The generalized Assmus-Mattson theorem for linear codes over finite fields developed in Tang, Ding and Xiong (2019) turns out to be useful, and will be the topic of a new chapter in this second edition.
It is well-known that MDS codes support only trivial designs (i.e., complete designs), which are not interesting. The Golay ternary code with parameters [11, 6, 5] is near MDS and supports a 4-design. It had been a 70-year-old open question whether there is an infinite family of near MDS codes over finite fields supporting an infinite family of 2-designs. Similarly, it was open for 71 years whether there is an infinite family of linear codes supporting an infinite family of 4-designs. The breakthroughs regarding these two open problems will be the main topic of another new chapter in this second edition.
In addition to the breakthroughs mentioned above, other progresses on designs from linear codes have been also made in the past three years. Based on these progresses, some chapters in the first addition were revised and new references were added.
In this second edition, a new appendix (named ) was also added for reporting some new sporadic 4-designs and 5-designs supported by some sporadic linear codes. In this second edition, notes are added at the end of most of the chapters for providing further information on the topics covered in the chapters.
We are very grateful to Dr. Yan Hong Ng, Dr. K. K. Phua and Ms. Kim Tan of World Scientific for helping us with the publication of this second edition. We acknowledge the financial support of the Hong Kong Research Grants Council, under Proj. No. 16300418.
Cunsheng Ding
Chunming Tang
Fall 2021
Preface to the First Edition
Linear codes and t-designs are companions. On one hand, the incidence matrix of a t-design generates a linear code over any finite field GF(q). On the other hand, the supports of codewords of a fixed Hamming weight in a code may form a t-design under certain conditions. Interplay between coding theory and the theory of t-designs has been a very interesting topic for combinatorialists and coding theorists, and has been treated to some extent in a few monographs and textbooks on coding theory and combinatorics. The purpose of this monograph is to give a comprehensive treatment of t-designs from linear codes. A special feature of this monograph is the attention to the determination of the parameters of t-designs held in linear codes.
The determination of the weight distributions of linear codes is an extremely difficult problem in general, and is much more difficult than that of the minimum weights of linear codes. The settlement of the parameters of t-designs held in a linear code over GF(q) is even harder when q > 2. A strong motivation of this monograph is the recent advance in the determination of the weight distributions of many families of linear codes. This monograph is a strong demonstration of the usefulness of the weight distributions of linear codes.
One may question the motivation of explicitly constructing designs with small strength. Our interest in explicit designs with small strength comes from the fact that they may yield linear codes with very good parameters, which could be very attractive in both theory and practice, although this monograph deals little with the linear codes of designs.
This monograph studies t-designs mainly from linear codes over finite fields. A few families of nonlinear codes do yield 3-designs. They include Goethals codes, Kerdock codes, and some extended perfect codes. The reader is referred to Tonchev (2007) for further information on designs from these families of nonlinear codes. Several families of t-designs have been constructed from codes over 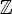 4. Information about these designs could be found in Helleseth, Rong and Yang (2001). These are the designs missing from this book.
4. Information about these designs could be found in Helleseth, Rong and Yang (2001). These are the designs missing from this book.












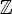 4 [Tanabe (2000)], and rank-metric codes [Byrne and Ravagnani (2019)]) were developed. The Assmus-Mattson theorem for matroids developed in Britz, Royle and Shiromoto (2009) does contain the original Assmus-Mattson theorem as a special case, but it becomes the Assmus-Mattson theorem when it is applied to codes. The generalized Assmus-Mattson theorem for linear codes over finite fields developed in Tang, Ding and Xiong (2019) turns out to be useful, and will be the topic of a new chapter in this second edition.
4 [Tanabe (2000)], and rank-metric codes [Byrne and Ravagnani (2019)]) were developed. The Assmus-Mattson theorem for matroids developed in Britz, Royle and Shiromoto (2009) does contain the original Assmus-Mattson theorem as a special case, but it becomes the Assmus-Mattson theorem when it is applied to codes. The generalized Assmus-Mattson theorem for linear codes over finite fields developed in Tang, Ding and Xiong (2019) turns out to be useful, and will be the topic of a new chapter in this second edition.