Inhalt
Guide

Zoran Stani
Regular Graphs
De Gruyter Series in Discrete Mathematics and Applications

Edited by
Michael Drmota, Vienna, Austria Jnos Pach, Lausanne, Switzerland Martin Skutella, Berlin, Germany
Volume 4

Mathematics Subject Classification 2010
05C50, 05C12, 05C76, 05C81, 05B05, 05B20, 65F15, 68R10, 94B05
Author
Prof. Dr. Zoran Stani
University of Belgrade
Faculty of Mathematics
Studentski trg 16
11000 Belgrade
Serbia
ISBN 978-3-11-035128-6
e-ISBN (PDF) 978-3-11-035134-7
e-ISBN (EPUB) 978-3-11-038336-2
Set-ISBN 978-3-11-035135-4
ISSN 2195-5557
Library of Congress Cataloging-in-Publication Data
A CIP catalog record for this book has been applied for at the Library of Congress.
Bibliographic information published by the Deutsche Nationalbibliothek
The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at http://dnb.dnb.de.
2017 Walter de Gruyter GmbH, Berlin/Boston
www.degruyter.com
Preface
This book has been written to be of use to scientists working in the theory of graph spectra. It may also attract the attention of graduate students dealing with the same subject area as well as all those who use graph spectra in their research, in particular, computer scientists, chemists, physicists or electrical engineers.
In the entire book we investigate exactly one class of graphs (regular) by using exactly one approach (spectral), that is we study eigenvalues and eigenvectors of a graph matrix and their interconnections with the structure and other invariants. Regular graphs appear in numerous sources. In particular, they can probably be encountered in all the books concerning graph theory. An intriguing phenomenon is that, in many situations, regular graphs are met as extremal, exceptional or unique graphs with a given property. More tangibly, an inequality is attained for a regular graph or a claim holds unless a graph under consideration is regular or it does hold exactly for regular graphs. In other words, depending on a given problem they fluctuate from one amplitude to another, which is making them probably the most investigated and the most important class of graphs, and simultaneously motivating us to consider the theory of graph spectra through the prism of regular graphs. There is also a relevance of regular graphs in the study of other discrete structures such as linear spaces or block designs. A final motivation for this book is a remarkable significance of regular graphs in branches of computer science, chemistry, physics and other disciplines that consider processes dealing with graph-like objects with high regularity and many symmetries.
The rapid development of graph theory in last decades caused an inability to cover all relevant results even if we restrict ourselves to a singular approach, so we must say that this material represents a narrowed selection of (in most cases, known) results. Our intention was to include classical results concerning the spectra of regular graphs along with recent developments. Occasionally, possible applications are indicated. The terminology and notation are taken from our previous book []. This book was written to be as self-contained as possible, but we assume a decent mathematical knowledge, especially in algebra and the theory of graph spectra.
Here is a brief outline of the contents..
Observing the table of contents, the reader may notice that expanders explored in which motivated us to set these two chapters next to one another.
All chapters are divided into sections and some sections are divided into subsections. The reader will also notice the existence of paragraphs that occur irrespectively of the above hierarchy.
Each of the ]. For details that are not presented here, we recommend some of these books.
The author is grateful to Tamara Koledin who read parts of the manuscript and gave valuable suggestions, and to Sebastian Cioab, Drago Cvetkovi, Edwin R. van Dam, Willem H. Haemers, Tamara Koledin again and Peter Rowlinson for permissions to reproduce some of their proofs without significant change. Finally, Nancy Christ, Apostolos Damialis and Nadja Schedensack on behalf of the publisher helped with editing the book by answering a lot of questions, which is much appreciated.
Last but not least, the author apologizes in advance for possible misprints or computational errors as well as for the inconvenience these might cause to the reader.
List of Figures
Fig. 3.1C6 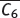 (top), its bipartite double (left) and extended bipartite double (right).
(top), its bipartite double (left) and extended bipartite double (right).
1Introduction
Here we give a survey of the main graph-theoretic terminology, notation and necessary results. The presentation is separated into three sections. In the first two we deal with graph structure and give some observations including statistical data on regular graphs. In the third section we focus on the adjacency matrix and the corresponding spectrum.
Since all parts of this chapter can be found in numerous sources, by the assumption that the reader is familiar with most of the concepts presented, we orientate to a brief but very clear and intuitive exposition. More details are given in the introductory chapter of our previous book [].
1.1Terminology and notation
Vertices and edges
Let G be a finite undirected simple graph (so, without loops or multiple edges). We denote its set of vertices (resp. edges) by V or V ( G ) (resp. E or E ( G )). In addition, we assume that |V|=0 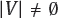 . The quantities n = | V | and m = | E | are called the order and the size of G , respectively. Two vertices u and v are adjacent (or neighbours ) if they are joined by an edge. In this case we write u ~ v and say that the edge uv is incident with vertices u and v . Similarly, two edges are adjacent if they are incident with a common vertex.
. The quantities n = | V | and m = | E | are called the order and the size of G , respectively. Two vertices u and v are adjacent (or neighbours ) if they are joined by an edge. In this case we write u ~ v and say that the edge uv is incident with vertices u and v . Similarly, two edges are adjacent if they are incident with a common vertex.
The set of neighbours (or the neighbourhood ) of a vertex v is denoted N ( v ). The closed neighbourhood of v is denoted N [ v ] (= { v } N ( v )).
Two graphs G and H are said to be isomorphic if there is a bijection between sets of their vertices which respects adjacencies. If so, then we write G H . Observe that the graphs illustrated in are isomorphic. In particular, an automorphism of a graph is an isomorphism to itself.
The degree d v of a vertex v is the number of edges incident with it. The minimal and the maximal vertex degrees in a graph are denoted and , respectively. A vertex of degree 1 is called an endvertex or a pendant vertex.
We say that a graph G is regular of degree r if all its vertices have degree r . If so, then G is referred to as r -regular. In particular, a 3-regular graph is called a cubic graph .
The complete graph with n vertices K n is the unique ( n 1)-regular graph. Similarly, the cocktail party CP ( n ) is the unique (2 n 2)-regular graph with 2 n ( n 1) vertices. The complete graph K is called the trivial graph .
The r-dimensional cube Q r is an r -regular graph of order 2 r with the vertex set V ( Q r ) = {0, l} r (all possible binary r -tuples) in which two vertices are adjacent if they differ in exactly one coordinate (see ).

















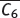 (top), its bipartite double (left) and extended bipartite double (right).
(top), its bipartite double (left) and extended bipartite double (right).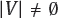 . The quantities n = | V | and m = | E | are called the order and the size of G , respectively. Two vertices u and v are adjacent (or neighbours ) if they are joined by an edge. In this case we write u ~ v and say that the edge uv is incident with vertices u and v . Similarly, two edges are adjacent if they are incident with a common vertex.
. The quantities n = | V | and m = | E | are called the order and the size of G , respectively. Two vertices u and v are adjacent (or neighbours ) if they are joined by an edge. In this case we write u ~ v and say that the edge uv is incident with vertices u and v . Similarly, two edges are adjacent if they are incident with a common vertex.